24 luty 07 (97)

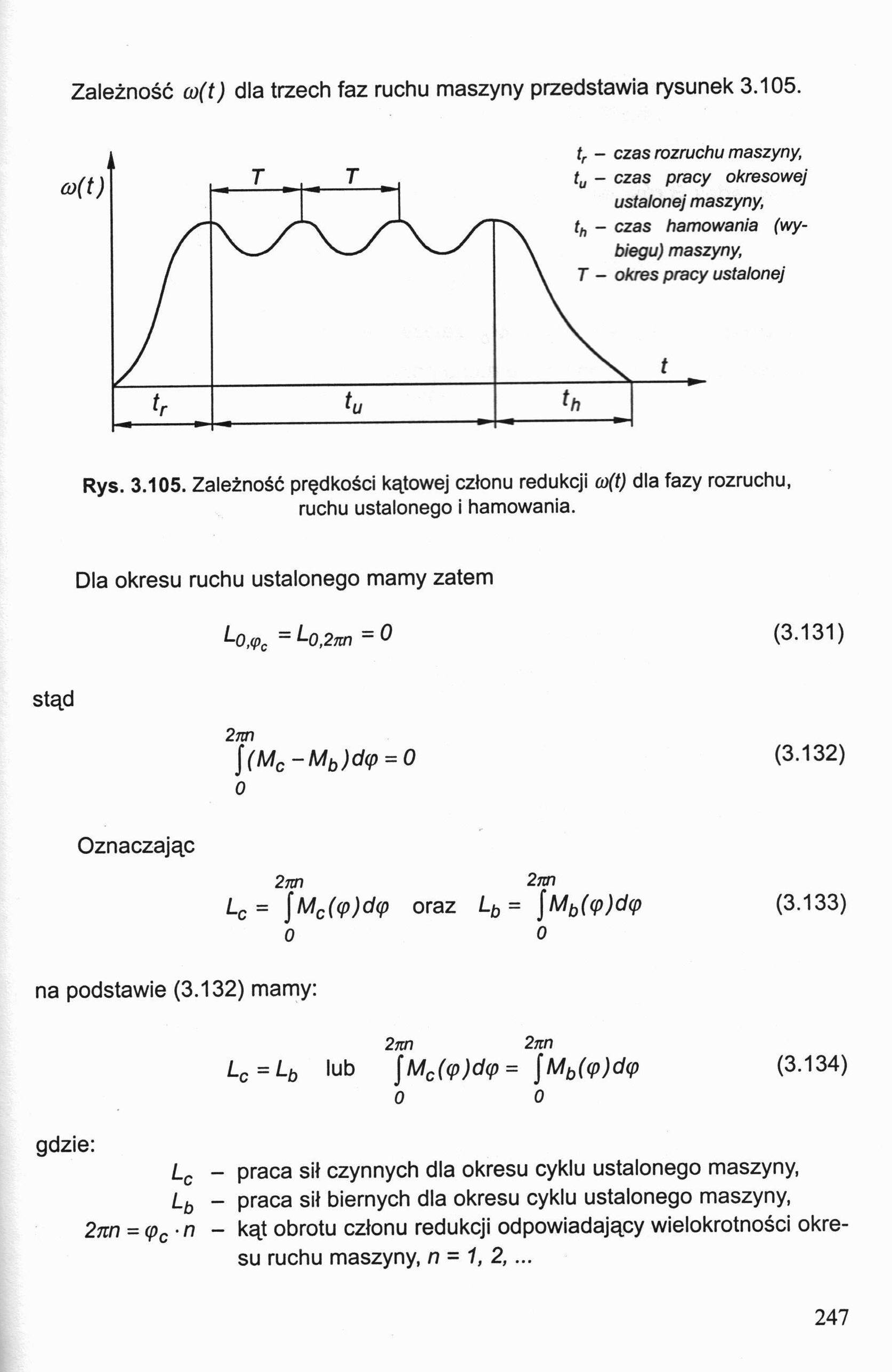
Zależność co(t) dla trzech faz ruchu maszyny przedstawia rysunek 3.105.

t_r - czas rozruchu maszyny, t_u - czas pracy okresowej ustalonej maszyny, t_h - czas hamowania (wybiegu) maszyny,

T - okres pracy ustalonej

Rys. 3.105. Zależność prędkości kątowej członu redukcji co(t) dla fazy rozruchu, ruchu ustalonego i hamowania.

Dla okresu ruchu ustalonego mamy zatem

L(),<p_c - l~0,2nn ~ 0

(3.131)

stąd

2rm

j(M_c-M_b)d(p = 0 0

(3.132)

Oznaczając

2nn    2nn

L_c= l^_c((P)dę oraz L_b = JM_b(cp)dę o    o

(3.133)

na podstawie (3.132) mamy:

L_c=L_b lub

2nn    2nn

jM_c((p)d(p= \M_b(ę)d(p 0    0

(3.134)

gdzie:

^Lb

2nn = ę_c-n

praca sił czynnych dla okresu cyklu ustalonego maszyny, praca sił biernych dla okresu cyklu ustalonego maszyny, kąt obrotu członu redukcji odpowiadający wielokrotności okresu ruchu maszyny, n = 1, 2,...

247