24 luty 07 (130)

stąd

^Jkp ~ J*

a>

zr

CO _r

4k'zr,i

(P3.274)

Ponieważ wał pośredni obraca się zwykle wolniej od wału silnika (co_zr = co_s > Wp), takie umiejscowienie koła zamachowego prowadzi do zwiększenia jego momentu bezwładności, a zatem i wymiarów.

Obliczenie wymiarów koła zamachowego wykonanego ze stali o gęstości p przeprowadzimy przy założeniu, że ma ono kształt pełnego walca o średnicy zewnętrznej D oraz szerokości b, a jego główna centralna oś bezwładności pokrywa się z osią obrotu.

W takim przypadku moment bezwładności koła wyliczymy ze wzoru

(P3.275)

.    1    ₂ 1 _n2 1 nD² .    -2 nD⁴b-p

j_k = —mr = —mD ---b-p-D =-—

* 2    8    8 4    32

Jeżeli założymy stosunek szerokości koła b do jego średnicy D: yr = —, wówczas jego moment bezwładności wynosi

Jk =

nD⁵y/ ■ p 32

(P3.276)

stąd

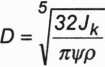
(P3.277)

Dla danych: J_k = 1,583 kg-m² (moment bezwładności koła obliczony w przykładzie 3.36), y/ = 0,2, oraz gęstości stali p = 7850 kg/m³, otrzymamy:

_{D = J}. 32 -1,583 _ _=0>40mi

n-0,2-7850 b = \f/-D = 0,2-0,40 = 0,08 m.

Masa koła wyniesie

= 79,15 kg.

8J_k 8-1,583

m = —— =---

D² 0,4²

280