24 luty 07 (68)

wzrosną wartości momentów bezwładności J_S1 i J_S2 członów 1 i 2, co spowoduje znaczny wzrost momentu bezwładności całego mechanizmu. Ponadto przeciwciężar m_k2 jest kłopotliwym elementem konstrukcyjnym.

Z wyżej wymienionych przyczyn w praktyce rzadko stosuje się całkowite wyrównoważanie statyczne. Stosuje się natomiast wyrównoważanie statyczne częściowe, które polega na tym, że nie sprowadza się wektora głównego sił bezwładności do zera, lecz dąży się do zmniejszenia jego wartości oraz odpowiedniego doboru jego kierunku.

Przykład 3.23

Wyrównoważanie statyczne częściowe mechanizmu korbowo-suwakowego.

Dany jest niewyrównoważony mechanizm korbowo-suwakowy jak w przykładzie 3.22. Przeprowadzić wyrównoważenie statyczne częściowe mechanizmu.

Rozwiązanie

Do wyrównoważenia mechanizmu zastosujemy tylko jedną masę korekcyjną m_k1 umieszczoną na przedłużeniu korby (rys. 3.88).

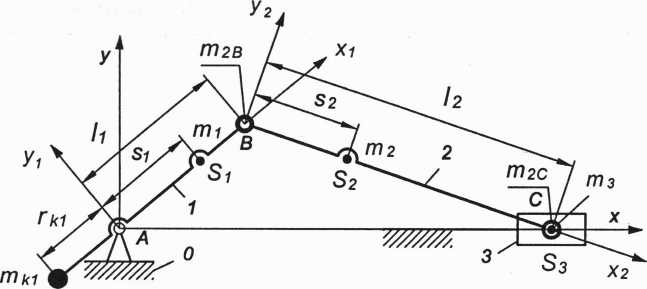
Rys. 3.88. Częściowe wyrównoważanie mechanizmu korbowo-suwkowego

W kroku pierwszym wyrównoważania zastępujemy masę członu 2 układem dwóch mas m_2B i m_2C skupionych w punktach B i C.

Wykorzystamy w tym celu metodę mas zastępczych.

Metoda mas zastępczych polega na zastąpieniu mas niektórych członów sztywnych (brył o ciągłym rozkładzie masy) skończonym zbiorem mas punktowych skupionych w wybranych z góry punktach w taki sposób, aby spełnić poniższe warunki.

218