24 luty 07 (131)

Analiza wzoru (P3.275) wykazuje, że na wartość momentu bezwładności koła zamachowego decydujący wpływ ma jego średnica zewnętrzna. Uzasadnione jest zatem rozmieszczanie masy koła na dużym promieniu. Koła zamachowe często projektuje się w kształcie pierścienia połączonego z piastą za pomocą konstrukcji żebrowej. Taka konstrukcja pozwala usunąć część masy koła, umieszczoną na mniejszej średnicy, która w małym stopniu wpływa na jego moment bezwładności.

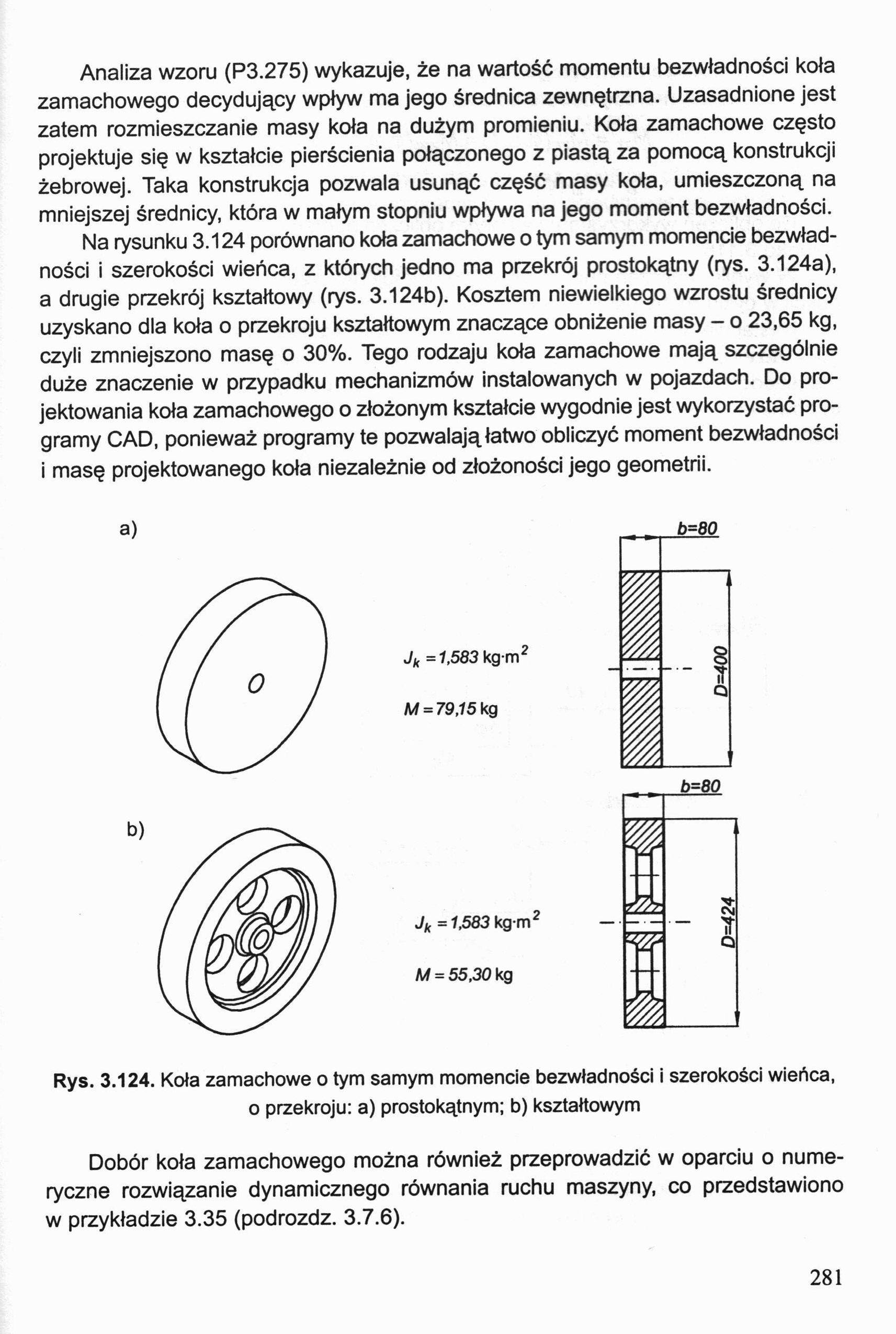
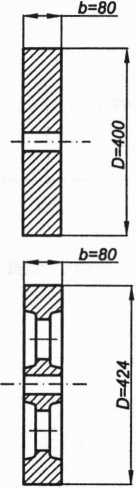
Na rysunku 3.124 porównano koła zamachowe o tym samym momencie bezwładności i szerokości wieńca, z których jedno ma przekrój prostokątny (rys. 3.124a), a drugie przekrój kształtowy (rys. 3.124b). Kosztem niewielkiego wzrostu średnicy uzyskano dla koła o przekroju kształtowym znaczące obniżenie masy - o 23,65 kg, czyli zmniejszono masę o 30%. Tego rodzaju koła zamachowe mają szczególnie duże znaczenie w przypadku mechanizmów instalowanych w pojazdach. Do projektowania koła zamachowego o złożonym kształcie wygodnie jest wykorzystać programy CAD, ponieważ programy te pozwalają łatwo obliczyć moment bezwładności i masę projektowanego koła niezależnie od złożoności jego geometrii.

a)

Rys. 3.124. Koła zamachowe o tym samym momencie bezwładności i szerokości wieńca, o przekroju: a) prostokątnym: b) kształtowym

Dobór koła zamachowego można również przeprowadzić w oparciu o numeryczne rozwiązanie dynamicznego równania ruchu maszyny, co przedstawiono w przykładzie 3.35 (podrozdz. 3.7.6).

281