24 luty 07 (78)

b)

W/M.

zr

zr

m

zr

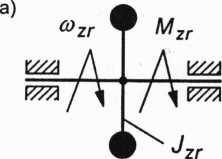
Rys. 3.95. Jednomasowe modele graficzne członów redukcji: a) człon redukcji w ruchu obrotowym: b) człon redukcji w ruchu postępowym

3.7.3. Redukcja mas i momentów bezwładności

Twierdzenie 3.3. Energia kinetyczna członu redukcji jest równa sumie energii kinetycznych członów ruchomych mechanizmu

E_zr = £E,    (3.90)

n=1

gdzie:

E_zr - energia kinetyczna członu redukcji, Ej - energia kinetyczna i-tego członu.

Ponieważ człony ruchome mechanizmu płaskiego mogą wykonywać ruch postępowy, obrotowy lub płaski podamy wzory na obliczanie energii kinetycznej w tych ruchach.

Wprowadźmy oznaczenia:

i = 1, 2, 3,...,n

^mi

m

zr

Joi ~

^Jzr

Vsi -(O, -Vzr ~ w -, -

liczba członów ruchomych, masa i-tego członu,

masa zredukowana (masa członu redukcji), moment bezwładności /-tego członu względem jego osi obrotu O_h

moment bezwładności i-tego członu względem osi przechodzącej przez jego środek masy S,-,

zredukowany moment bezwładności ( moment bezwładności członu redukcji),

prędkość liniowa środka masy i-tego członu, prędkość kątowa i-tego członu, prędkość liniowa członu redukcji, prędkość kątowa członu redukcji.

228