274 2

274

7. Różnice skończone w całkowaniu i różniczkowaniu

Jeśli natomiast węzły ustawimy w kolejności

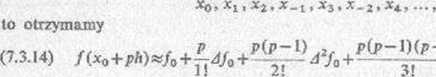
p(j>-l)(p~2)

----r:-1 +

+

(P+0j»(/>-l>(p-2) ^ 4!

Obcinając te rozwinięcia na różnicy nieparzystego rzędu, otrzymuje się i w (7.3.13) i _v (7.3.14) ten sam wielomian interpolacyjny; rozwinięcia mają inną postać, ale wykorzystują te same wartości funkcji. Nie byłoby tak natomiast w przypadku obcięcia rozwinięć na różnicy parzystego rzędu, gdyż np. rozwinięcie (7.3.13) zakończone różnicą A² korzysta z wartości w węzłach *_ _l5 x_Q i x_x. a rozwinięcie (7.3.14) - z wartości w węzłach x₀, _tX Powyższe dwa wzory nazywa się niekiedy wzorami Newtana-Gaussu. Wzór famełn jest ich średnią arytmetyczną.

7.3.5. Dodatkowe uwagi o interpolacji

Interpolacja jest ważna jako sposób konstrukcji wzorów służących do różnych celów. Różniczkując lub całkując wielomian interpolacyjny, otrzymuje się użyteczne metody obliczania numerycznego pochodnych lub całek.

Prócz tego interpolacja wyższych stopni ma bezpośrednie zastosowania praktyczne, gdyż pozwala znacznie zmniejszać tablice funkcji w porównaniu z tymi, które są potrzebne w razie używania interpolacji liniowej.

Przykład 7.3.3. (Zaczerpnięty z [31], ćwiczenie 10.5.7.) Tablica funkcji łnx dla K śxś:5, w której wartości mają pięć cyfr ułamkowych, iftusi zawierać 450 pozycji, jeśli zakłada się korzystanie z interpolacji liniowej i tylko 100 pozycji w przypadku posługiwania się interpolacją kwadratową. (Przyjmujemy tu pewne sensowne założenia o wielkości kroku w tablicy i częstości jego zmiany oraz żądamy, aby łączny błąd interpolacji nie przewyższał i Cr⁵.)

• Dla tablic używanych szczególnie często wygoda korzystania z nich jest oczywis^⁶ ważniejsza niż ich małe rozmiary. Natomiast dla tablic używanych rzadko, 3 dokładnych (np. dziesięcio- lub piętnastocyfrowych), zwartość tablicy jest często n^b&r

dziej istotna. (Takie wielocyfrowc tablice przydają się niekiedy do testowania

Iromnn tern wvełi. \

k^uincj łYjRyizysuił,    ucuuKuwtu, uo iiuiiunum iiwuy ---

tycznych (potrzebnych do obliczania wartości funkcji).

rytn*-