304 2

304

?. Różnice skończone w całkowaniu i różniczkowaniu

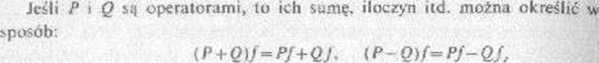
^nab{VPUjący

{PQ)fmP(Qf I. (xP)f=a(PJ),

F¹/- PP...Pf (n czynników).

Za u walmy, że

(Dwa operatory są równe, czyli P= Q, jeśli Pf-Qj dla każdej funkcji /). Można wy kazać, że dla dowolnych operatorów liniowych są słuszne następujące prawa:

P+Q~Qą-P, P+(G + KMtP+Q)-ł-tf.

PiO + R)-PQ + PR. P(QR)=(PQ)R

Wszystkie operatory, które będziemy rozważali, są przemienne: PQ — QP. Można też wykazać, że słuszne są pozostałe aksjomaty określające pierścień. Z 3lgebry wiadomo, że twierdzenie o dwumianie Newtona można wyprowadzić z podstawowych aksjomatów takiego pierścienia. Jeśli zatem k jest liczbą całkowitą dodatnia, to wzory (7.6.1) są szczególnymi przypadkami ogólniejszych twierdzeń algebry.

7.6.2. Szeregi operatorowe i ich zastosowania

Wyjdziemy teraz poza algebrę i rozpatrzymy szeregi nieskończone operatorów. Szereg Taylora

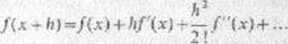
można napisać symbolicznie w postaci

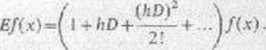
Wynika stąd następujące twierdzenie:

TwiFRDZENIE 7.6.1. (7.6.2)

Ten piękny wynik jest podstawą dalszych rozważań.

Przykład 7.6.1. Z wzorów (7.6.1) i (7.6.2) wynika, żc

e*^D-l +A .