312 2

312

7. Różnice skończone w całkowaniu i różniczkowaniu

Bardzo ważnym w fizyce operatorem różniczkowym jest laplasjan F^a:

(7.7.6)

, d^zu d*u ^{F U}~dx³*dy²

(Podkreślamy, że V nie jest tu operatorem różnicy wstecznej, natomiast oznacza gradient (d/dx, ojoy).) Laplasjan można przybliżać na wiele sposobów. Załóżmy, że k=k v» • prostszym przybliżeniem jest wtedy operator pięciopmktowy V\ określony wzorem ^

(7.7.7)

w.-.jł, —2tt_l7+u, y_,

i schematycznie pokazany na rys. 7.7.2. Z wzoru (7.1.13) wynika, że

-4..    ₅4.

,    _?    1 , /c u ć u\ .

^ri“'>“^⁺T2^AV⁺e?)^+0(ft)

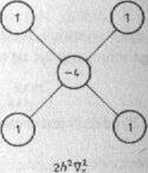
Rys. 7.7.2    Rys. 7.7.3

Inny operator różnicowy oznaczymy symboicm V\:

_nl    tył 1.7+1 +    '^rWi+ I./- 1 + ^u.-IJ-t-ł“4tfy

-----2A*-

(zob. rys. 7.7.3). Można wykazać, że

₂ri

Pi _Uij=P^ ₊ ,^_T_₊^_₊_jJ ₊ 0(/, ).

I    Pą’

Kombinacja liniowa tych dw^róeh operatorów daje operator dziewięciopunktowy

Odpowiada mu schemat z rys. 7.7.4. Ten operator jest w wielu sytuacjach użyte*®¹? (8.6.10) i zadanie 8 z § 8.6) ze względu na szczególną postać reszty:

(7.7.8)

F;_m>v~F²k + ~/,V⁴u + 0(7»⁴).