368 (15)

368 10. Obliczanie parametrów obwodów elektrycznych

SS*&n.

y = y-r

Po podstawieniu do wzoru (10.56b) otrzymuje się

^k+2nk²+^k²

W~

przy czym

— W przedziale trzecim bezpośrednio ze wzoru (10.56c) wynika, że

HH Ig

— W przedziale zaś czwartym

= 2rcosa^/ dy = r cos a* da'

zatem

O fda' 1 , WflW — J 2 ~2°'

Ponieważ

WMŚ

więc

i.    1

⁼2^arCCOSb

— W przedziale piątym podobnie, jak w trzecim

Ostatecznie więc przewodność magnetyczna jednostkowa żłobka 0,351 + WMMI 2n+ — \k²

W ~

1

■

+ —=■ + -arccos-^- +

b,

(10.58)

W podobny sposób można wyprowadzić przybliżone wzory na przewodność magnetyczną jednostkową żłobków o innych kształtach. Między wynikami obliczeń wykonanych przy założeniu prostoliniowego przebiegu linii pola w żłobku a wynikami badań wykonanych na modelach występuje jednak znaczna rozbieżność — zwłaszcza w przypadku żłobka o przekroju kołowym (rys. 10.6c). Dla całkowicie zapełnionego żłobka o przekroju kołowym otrzymuje się z zależności (10.56b) przewodność

Według Annella [10.1] natomiast

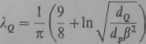
przewodność zależy od stosunku średnicy żłobka d_g do średnicy przewodu d_p oraz od kąta rozwarcia żłobkowego 2p — rys. 10.6c. Przyjmując d_g/d_p ~ 1, otrzymuje się wzór

(10.5%)

A_fl = ^(l,125-ln/ł)

Wartości obliczone wg tego wzoru są praktycznie zgodne z otrzymywanymi z prostszej zależności podanej przez Rotherta na podstawie badań modelowych

A_fl = 0,47 +0,066^

Di

(10.60)

1

Dla przestrzeni zajętej przez uzwojenie w żłobku o przekroju trapezowym otrzymuje się [10.3] — rys. 10.6d i rys. 10.6e

(10.61 a)

przy czym dla żłobka stojana

(10.61b)

,4t²-t*(3-41nt)-l **^{() = 3} 4(t¹—l)^ł(t—1)

(10.61c)

Podobną zależność otrzymuje się dla żłobka wirnika — tabl. 10.4.

W pracy [4] wykazano, że dla wartości parametru 1 $ t < 2, zarówno dla żłobka wirnika, jak i stajana, współczynnik k, różni się od 1 nie więcej niż 5%. Można zatem przewodność żłobków trapezowych z płaskim dnem obliczać z prostszych wzorów przybliżonych — tabl. 10.4.

14 PrcjcŁlowMle mauyn cteUn-cttlrói