1636660690

1. Błędy obliczeń numerycznych 11

całki oznaczonej jako granicy sum przybliżających ją podziałów itp.),

d)    uproszczenie modelu matematycznego (przyjęcie założeń upraszczaj ący ch),

e)    błędy programisty.

1.2.2. Błędy względne i bezwzględne

Załóżmy, że wartość x jest reprezentowana jako x . Wówczas:

•    błąd bezwzględny reprezentacji jest równy x - x.

•    błąd względny [%] reprezentacji jest równy ——— • 100%, x ^ 0.

x

Przyjmijmy, że zapis x = x±s oznacza, że |3t-x|<s. Wartość

e = max|x -jc| nazywamy maksymalnym błędem bezwzględnym lub

błędem granicznym.

Mówiąc o liczbie cyfr istotnych w ułamku dziesiętnym nie uwzględnia się zer na początku tego ułamka, gdyż określają one tylko pozycję kropki dziesiętnej. Natomiast cyfry ułamkowe są to wszystkie cyfry po kropce dziesiętnej, także ewentualne zera.

Jeśli

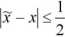
•10', to mówimy, że x ma t poprawnych cyfr

ułamkowych. Cyfry istotne występujące aż do pozycji t-tej po kropce nazywamy cyframi znaczącymi.

Przykład 1 A.

W kolejnych przykładach podano liczby odpowiednich cyfr: 0.00147 - 5 cyfr ułamkowych, 3 cyfry istotne,

12.34 - 2 cyfry ułamkowe, 4 cyfry istotne,

0.001234 ±0.000004 - 5 cyfr poprawnych, 3 cyfry znaczące, 0.001234 ± 0.000006 - 4 cyfry poprawne, 2 cyfry znaczące.

1.2.3. Przenoszenie się błędów

Przenoszenie się błędów numerycznych najlepiej zobrazuje przykład 1.2.

Przykład 1.2.

Niech x, = 2.31 ± 0.02, x₂ = 1.42 ± 0.03.