92737

Chemia fizyczna - termodynamika molekularna 2010/2011 50

nadmiarowa entropia nie może znikać. Ściśle zatem mówiąc, roztwór regularny nie istnieje -pojawienie się udziału entalpowego w funkcji G*' wnosi swój wkład do nadmiarowej entropii. W praktyce posługujemy się pojęciem roztworu regularnego dla takich układów, w których wpływ nadmiarowej entropii na G* jest pomijalnie mały w porównaniu z udziałem nadmiarowej entalpii.

Zagadnienie znalezienia konfiguracji równowagowej rozwiązuje się dwojako. Obie metody są przybliżone.

2. Przybliżenie kwazychemiczne, czyli pierwsza aproksymacja. Opiera się na zależności g(Nij) zaproponowanej przez Guggenheima. Jest to wyrażenie przybliżone. Funkcja dokładna jest na tyle skomplikowana, że nie może być stosowana w praktycznych zastosowaniach. W wyniku podstawienia do równania (3) otrzymuje się nieliniowy układ równali (układ kwazychemiczny). który należy rozwiązać względem Nij. Dość zaskakująca postać końcowych równali tłumaczy nazwę metody - patrz poniżej

JOL

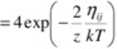
(5)

Widać tutaj analogię do równości pomiędzy ilorazem reakcji (lewa strona) i stałą równowagi rcakcji chemicznej (prawa strona). Stąd właśnie bierze się nazwa „kwazychemiczny". Przypominam, że powstawanie kontaktów' ij można przedstawić jak proces

Przybliżenie kwazychemiczne stanowi eleganckie rozwiązanie problemu znalezienia funkcji podziału dla roztworu regularnego. Jego wadą jest dość skomplikowana forma równań modelowych, szczególnie dla układów złożonych z dużej liczby różnych segmentów.

Jak widać z równania (5). liczby kontaktów zależą od energii oddziaływali pomiędzy nimi. Tak więc stężenia lokalne (bezpośrednio wokół segmentu) różnią się od stężeń średnich.

3.    Prostsza (i mniej ścisła metoda) nosi nazwę przybliżenia Brugga-Willianisa. czyli zerowej aproksymacji.

Zakłada się, że pomimo niezerowych energii wymiany, udział kombinatoryczny nie zależy od konfiguracji. Może być zatem taki sam jak w roztworze doskonałym czy atermalnym. Natomiast konfigurację równowagową wyznacza się ignorując różnice pomiędzy stężeniami lokalnymi a średnimi. Czyli przy założeniu swobodnego mieszania.

4.    Wyznaczenie równowagowej konfiguracji w przybliżeniu Bragga-Williamsa.

Spośród zq, zewnętrznych kontaktów cząsteczki i. średnio będzie zNifii/z&ijNj kontaktów typu M*. W ogólnym zatem przypadku musi być

zti (i N N

=    ' * ’ ¹ = Z0,0, N    dla kontaktów pomiędzy segmentami typu i-k

gdzie 0, jest ułamkiem kontaktów zewnętrznych określonego typu. zdefiniowanym jako