92739

Chemia fizyczna - lermodyiutmika molekulartui 2010/2011 13

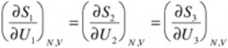
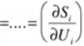
N.V

4. W stanie rozważanej równowagi, wszystkie układy charakteryzują się zatem taką samą wartością powyższych pochodnych. Jak widać, pochodne te mają duże znaczenie. Jak wiadomo z kursu podstawowego termodynamiki, pochodna ta stanowi definicję temperatury

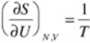
5. Inna definicja zespołu kanonicznego - jest to zbiór układów różniących się mikrostanami kwantowymi, a charakteryzujących się stałą wartością parametrów N,V,T.

6. Zespół kanoniczny można rozszerzyć uzmicnniając liczbę cząsteczek N. zachowując wymóg izolacji całego zbioru i istnienie wzajemnej równowagi pomiędzy układami. Uzyskujemy wtedy wielki zespół kanoniczny.

Podobne wyprowadzenie doprowadzi do stałości temperatury oraz stałości poniższej pochodnej

consl

m,r

dla każdego układu.

u.

Pochodna ta to oczywiście -£■ (udowodnić !). jeśli prawdziwe jest nasze podejrzenie, że

entropia statystyczna jest równoważna entropii fenomenologicznej, zdefiniowanej poprzez II Zasadę.

A zatem można oczekiwać, że wielki zespół kanoniczny to zbiór układów różniących się mikrostanami. a zachowujących tę samą wartość fi.V.T. W przypadku układu wieloskładnikowego, zawierającego cząsteczki różnego rodzaju, można zbudować zespół, w którym stałe są wartości potencjałów chemicznych wszystkich składników.

7.    Oczywista (rodność w posługiwaniu się innymi zespołami niż mikrokanoniczny polega na tym, że zasada równych prawdopodobieństw obowiązuje dla zespołu mikrokanonicznego. Aby ułatwić sobie życie sięgnijmy do uzupełnień z matematyki.

8.    Dla rozkładu prawdopodobieństwa (P1.p2.--Pn) definiuje się funkcję zwaną entropia informacji (S)

S = - k V p_t In p_t gdzie k jest stałą proporcjonalności.

Znaczenie entropii informacji wynika z następującego twierdzenia:

Najbardziej prawdopodobny (przypadkowy) rozkład prawdopodobieństwa odpowiada maksymalnej wartości entropii informacji.

Im niższa entropia, tym większa ilość informacji i mniej przypadkowy rozkład. Najbardziej przypadkowy (równomierny) odpowiada największej wartości entropii informacji.