3582327821

Chemia fizyczna - termodynamika molekularna 2010/2011 20

Wykład 6 (skrócony)

12.11.2010

1. Kontynuujemy całkowanie przy obliczaniu cząsteczkowej funkcji podziału dla jednoatomowego gazu doskonałego.

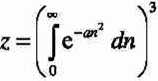
(2xmkTY²

< h² >

co wynika ze wzoru na poniższą całkę oznaczoną

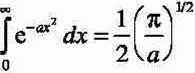
Uwaga! Zastąpienie sumy przez całkę nie zawsze jest uzasadnione. Błąd, który popełniamy przy tej operacji jest tyra mniejszy im mniejsza jest wartość parametru a. Dobrą dokładność zapewniają „odpowiednio” wysokie temperatury i „odpowiednio” duże masy cząsteczek. W praktyce oznacza to konieczność bezpośredniego sumowania dla cząstek elementarnych (nawet dla wysokich temperatur) oraz dla wodoru i helu dla niskich temperatur. Jeśli pominiemy temperatury niezmiernie bliskie zeru bezwzględnemu, dla wszystkich pozostałych sytuacji całkowanie zapewnia wystarczaj ącą dokładność.

Ostatecznie więc funkcja podziału dla N jednoatomowych cząsteczek czystego gazu doskonałego powinna wynosić

^(2iunkT\^w\_7N _ V»

l h² J A^3N

gdzie

(27tmk T)^m

Parametr A nosi nazwę długości termicznej fali de Broglie'a.

Znak zapytania pojawił się dlatego, że bardziej szczegółowa analiza funkcji podziału sugeruje jej niepoprawność (a jednak!). Nie przywiązujmy się zatem do tej formy, ponieważ będzie musiała być skorygowana.

2. Ale sprawdźmy, czy rzeczywiście prowadzi ona do właściwego równania stanu. To ostatnie wynika z elementarnej tożsamości termodynamicznej

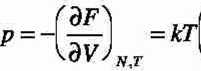
3lnZ

dV

N,T

Stąd, dla InZ = Mn V - 3NhxA(T) otrzymujemy NkT