3582327800

Chemia fizyczna - termodynamika molekularna 2009/2010 42

Wykładll

18.12.2008

1. Roztwór doskonały w świetle teorii siatkowej.

Zakładamy:

1)    Zerowanie energii wymiany.

2)    Jednakowy kształt cząsteczek różnego rodzaju (każda z nich zajmuje jeden węzeł sieci). Konfiguracyjna funkcja podziału będzie miała postać

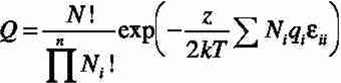
i=1

gdzie N = IN i. Iloczyn w mianowniku wynika z nierozróżnialności cząsteczek. Logarytmując i stosując przybliżenie Stirlinga otrzymujemy to e = N to N - N - £ N, ta AT, + £ AT, czyli

lne = WtoJV-XJV,toJV,-^|_rX^iv<«A

2. Potencjał chemiczny wyznaczamy poprzez różniczkowanie po liczbie cząsteczek. Ściśle mówiąc jest to jego część konfiguracyjna.

= -kT

f *F\    ,jf dlng^

^ ^dN* ' ry,N_itt li_k/kT = -(hiN+l-hiN_k-l-^q_kE_kk)

—kTlax_k +“#*£**

~—q_kc_& (potencjał chemiczny dla czystego składnika) I ostatecznie

P-* (2™, p,x_k) = p°(r, p) + RZln**

po przejściu do molowego potencjału chemicznego.

Otrzymany wynik jest ogólny i nie ogranicza się tylko do konfiguracyjnej funkcji podziału. Pozostałe elementy funkcji podziału (wynik całkowania po pędach oraz udziały kwantowe) są takie same dla cząsteczki w czystym składniku jak i w mieszaninie i ulegną wykasowaniu podczas wyprowadzenia. A to dzięki temu, że powyższe równanie ma charakter różnicy potencjałów pomiędzy dwoma stanami - składnikiem w mieszaninie i czystą substancją.

3. Otrzymujemy ostatecznie równanie opisujące potencjał chemiczny składnika w roztworze doskonałym, zgodne z jego definicją fenomenologiczną. Założenia, które zostały przyjęte na początku wyprowadzenia, stanowią zatem warunki doskonałości w świetle teorii siatkowej. Są one mniej restrykcyjne niż w tradycyjnej molekularnej interpretacji roztworu doskonałego, gdzie wymaga się, aby wszystkie oddziaływania pomiędzy cząsteczkami były sobie równe.