Fizyka – Wykład Część I

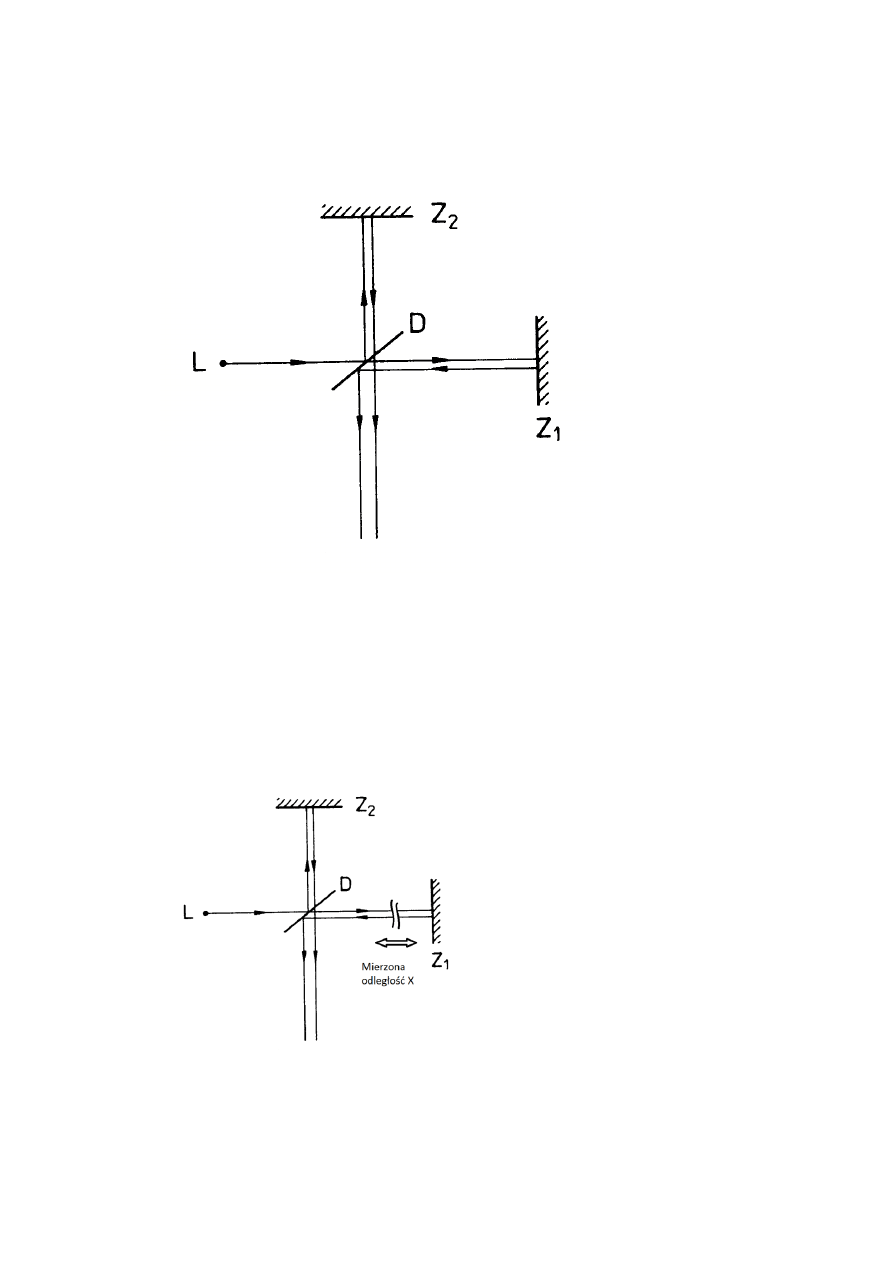
1. Interferometr Michelsona.

Mierzona jest różnica pomiędzy fazami..

o

Gdy spotykające się fale są o tej samej fazie, fale się wzmacniają

o

Gdy spotykające się fale są o przeciwnej fazie, fale się wygaszają

2. Do czego służy teraz interferometr Michelsona.



Pomiar współczynnika załamania w różnych ośrodkach
Pomiar prędkości światła w różnych ośrodkach



Precyzyjny pomiar odległości

3. W jaki sposób wykorzystać można interferometr Michelsona do pomiaru odległości.

Zwierciadło daje się na początku mierzonej odległości, a później na końcu.

4. W jaki sposób wykorzystać można interferometr Michelsona do pomiaru załamania.

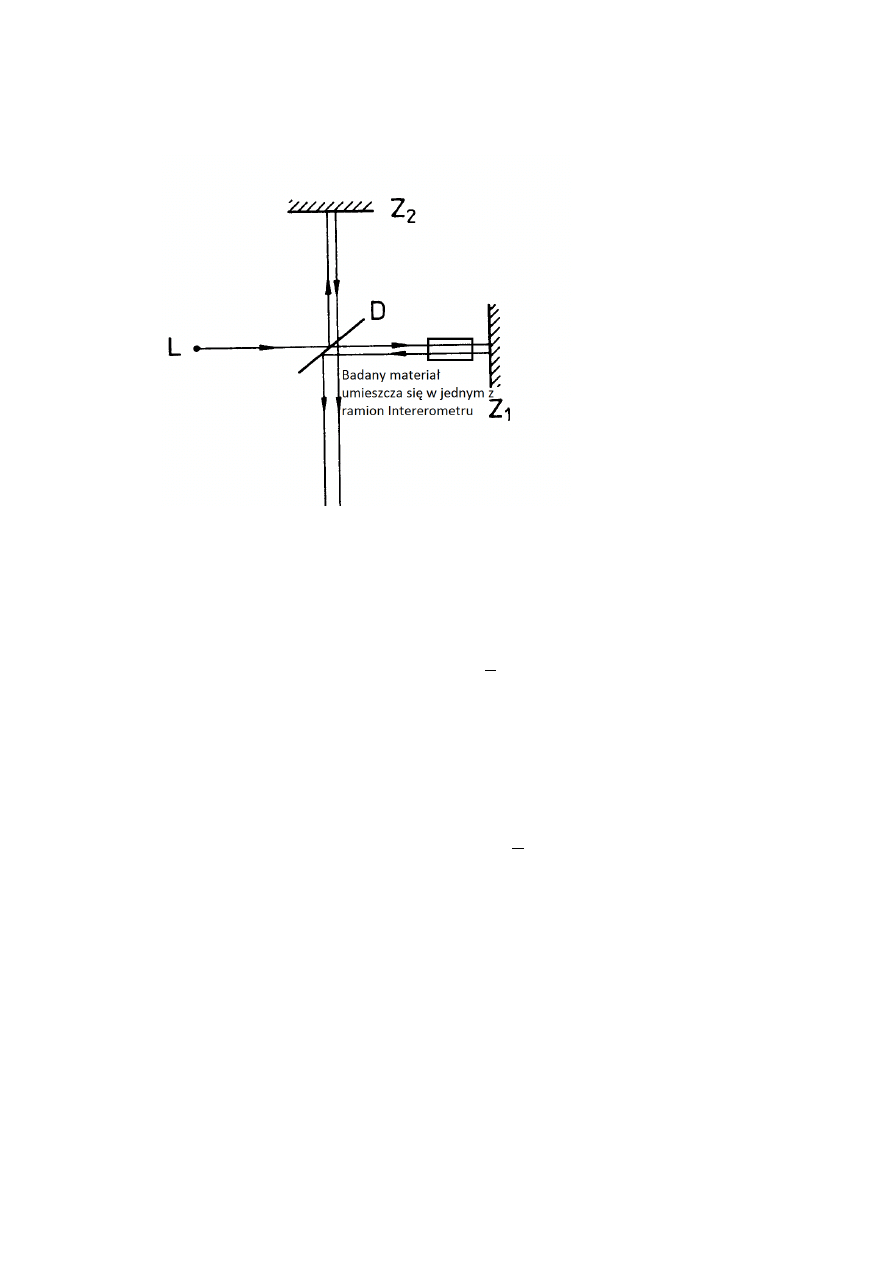
Jedno zwierciadło umieszcza się między układem interferometru, a danym ośrodkiem.

5. Zmiana fazy fali na przeciwną następuje w różnicy dł. fali o π .

6. Współczynnik załamania

ῃ =

𝑐

𝑣

gdzie
c-prędkość światła v-prędkość Światła w danym ośrodku

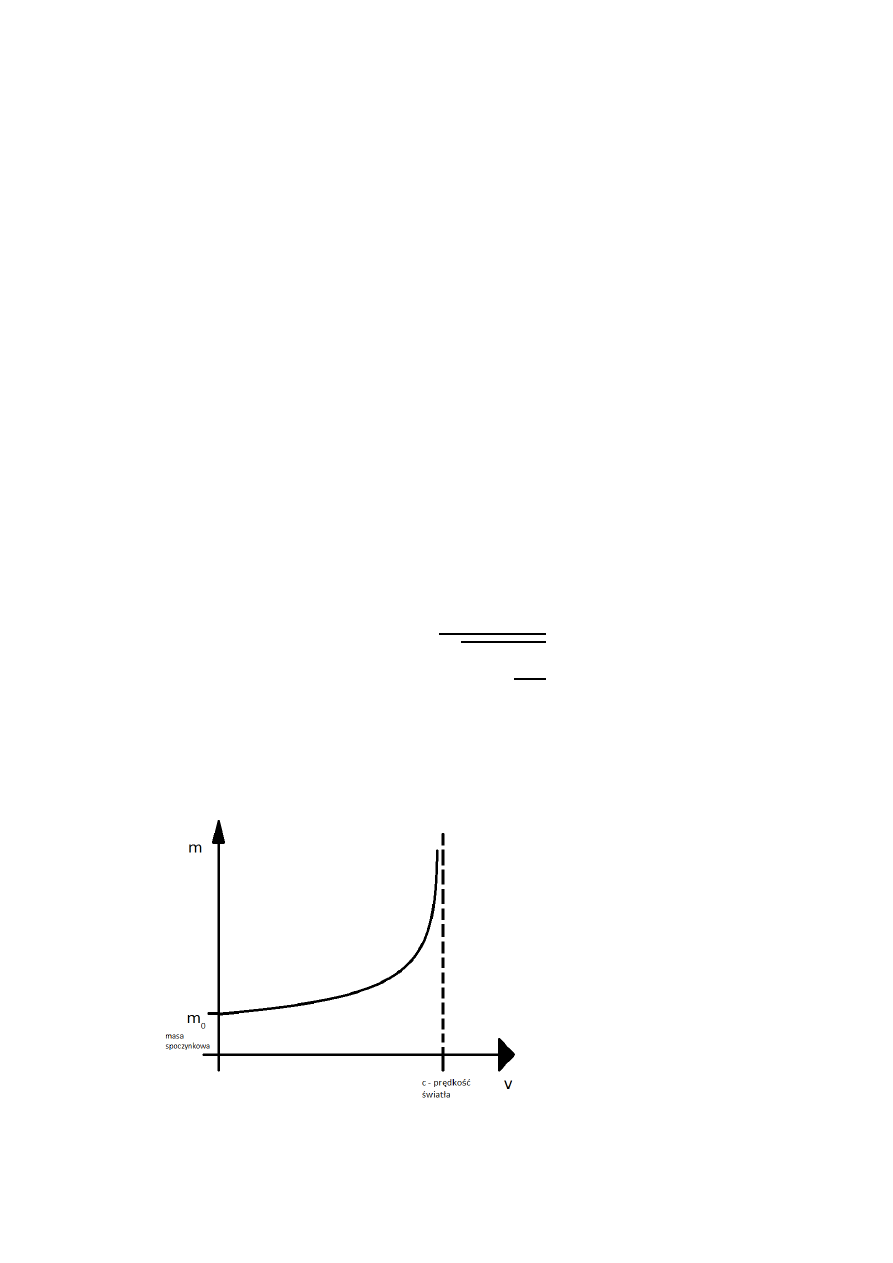
7. Oddziaływania między cząsteczkami przenoszą się poprzez odpowiednie pola ze

skończoną prędkością, nie przekraczając stałej uniwersalnej jaką jest prędkość światła
w próżni.

𝐶 = 3 ∗ 10

8

[

𝑚

𝑠

]

8. Fizyka kwantowa

fizyka klasyczna

Fizyka relatywistyczna

Fizyka nierelatywistyczna

V<<C

(Prędkości są znacznie mniejsze, od C)

9. Hipoteza Planca.

Wytłumaczenie rozkładu widmowego natężenia promieniowania termicznego ciała
doskonal czarnego.

E=h*v

Gdzie

E-energia

h-stała planca

v-częstotliwość drgań światłą

10. Stała Planca h posiada skończona wartość w teorii kwantowej ,natomiast w fizyce

klasycznej jest niskie (skończona wartość działania).
Najmniejszą porcją działania czyli kwant jest stała Planca.

11. Kiedy można korzystać z wzorów fizyki klasycznej, a kiedy kwantowej?

Kiedy wartości są zbliżone do najmniejszej porcji działania to używany wzorów
Fizyki kwantowej, w przeciwnym razie korzystamy ze wzorów fizyki klasycznej

12. Zasada odpowiedzialności Bohra.

Przewidywania teorii kwantowej dotyczące układu fizycznego muszą w pewnych
granicach odpowiadać przewidywaniom fizyki klasycznej.

13. Co dało doświadczenie Michelsona?

Szczególną teorię względności

14. Układ inercjalny

jest to układ który spoczywa lub porusza się ruchem jednostajnym

prostoliniowy

- nieinercjalny- jest to układ który nie spoczywa i nie porusza się ruchem jednostajny

prostoliniowym,

działają w nim siły bezwładności(siły d’alemberta)

15. Jakie są założenia „szczególnej” teorii względności”.



Prawa fizyki są jednakowe we wszystkich układach inercjalnych,



prędkość światła w próżni nie zależy od ruchu jego źródła,



Nie można przesłać informacji z prędkością większą od prędkości światła w
próżni,

16. Czemu teoria względności jest „szczególna”.

Ponieważ opisuje obserwacje jakie można przeprowadzić w ściśle określonych
warunkach. Dotyczy układów jednorodnych.

17. Prędkość światła w próżni zależy od przenikalność elektrycznej/magnetycznej

18. Różnica pomiędzy transformacją Lorentza a Galileusza

Galileusz-wszystkie czasy niezależne od układu są równe
Lorentz-czas zależy od układu
Nie uwzględnia transformacji czasu.*( nie uwzględnia się różnic w czasie)

19. Co to jest dylatacja czasu. (Na czym polega dylatacja czasu.)

Wnioski Lorentza

∆t

1

=ɣ∆t

2

Odstęp czasu ∆t

2

mierzony między dwoma zdarzeniami przez ruchomego obserwatora

jest krótszy niż odstęp czasu ∆t

1

mierzony przez obserwatora nieruchomego. (Czas

własny płynie wolniej)

20. Co to jest kontrakcja.

Wnioski Lorentza

∆x

1

=ɣ∆x

2

Odległość ∆x

1

mierzona w układzie względem którego punkty spoczywają jest

większa niż odległość ∆x

2

mierzona w układzie poruszającym się względem tych

punktów.

21. Wzór Einsteina

𝐸 = 𝑚𝑐

2

E-energia całkowita
m-masa relatywistyczna
c-prędkość światła w próżni

22. Masa relatywistyczna zależy od prędkości tego ciała,

Masa relatywistyczna zależy od prędkości tego ciała.

𝑚 =

𝑚𝑜

√1 −

𝑣

2

𝑐

2

m

o

– masa spoczynkowa

23. Wykres zależności masy relatywistycznej od prędkości

Równoważność energii w masie znalazła praktyczne zastosowanie w np.
elektrowniach jądrowych.

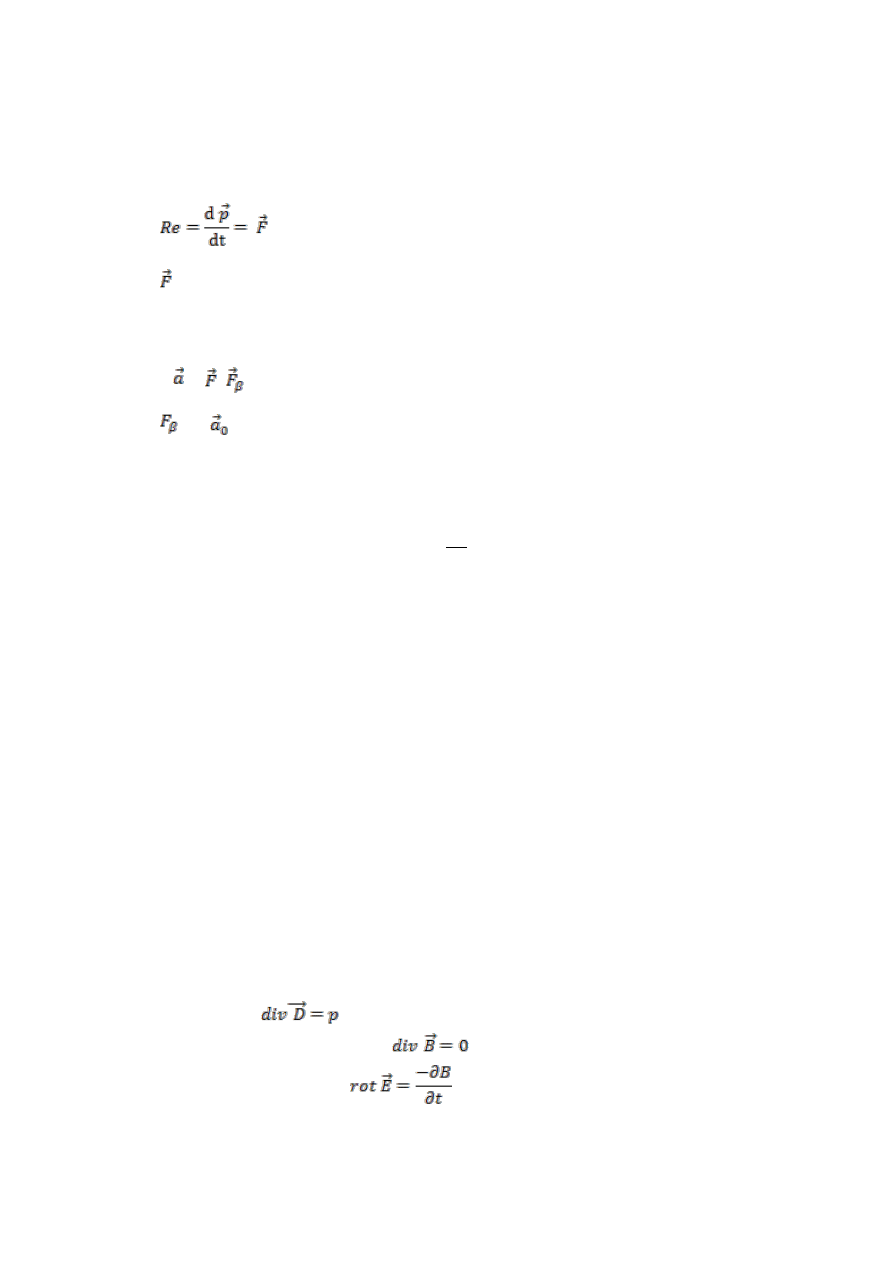
24.

II prawo ruchu postępowego w inercjalnym układzie współrzędnych.
Pod wpływem niezrównoważonej siły F następuje zmiana w czasie pędu p ciała określona
wzorem:

Pęd oraz siła F to Wektory!

= m*a

W mechanice relatywistycznej F w ogólnym przypadku nie jest równoległe

do a.

W nieinercjalnym:

m

2

= +

= -m

(siła bezwładności – siła d’Alamberta.

Ad 25. 1 Zasada dynamiki.

𝑑p

𝑑t

= 0

Cało pozostaje w spoczynku lub porusza się ruchem jednostajnie prostoliniowym.

3 Zasada dynamiki.
F

ij

= -F

ij

Siła akcji jest równa sile reakcji która jest o przeciwnym zwrocie.

25. Niezmiennikami transformacji Lorentza nie są



masa relatywistyczna oraz energia całkowita E oraz



siła F.

Ich wartość zależy od układu, w którym dokonywane są pomiary.

26. Niezmienniki transformacji Lorentza.



Interwał czasoprzestrzenny,



Ładunek elektryczny,



Równania Maxwella,

27. Niezmiennikiem transformacji Galileusza jest odległość w przestrzeni.
28. Równania Maxwella

Prawo Gaussa

Źródłem pola elektrycznego są ładunki elektryczne.

Prawo Gaussa dla magnetyzmu:

Pole magnetyczne jest bezźródłowe.

Prawo indukcji Faradaya:

Wiry pola elektrycznego powstają w miejscach w

których następuje zmiana w czasie indukcji pola magnetycznego.

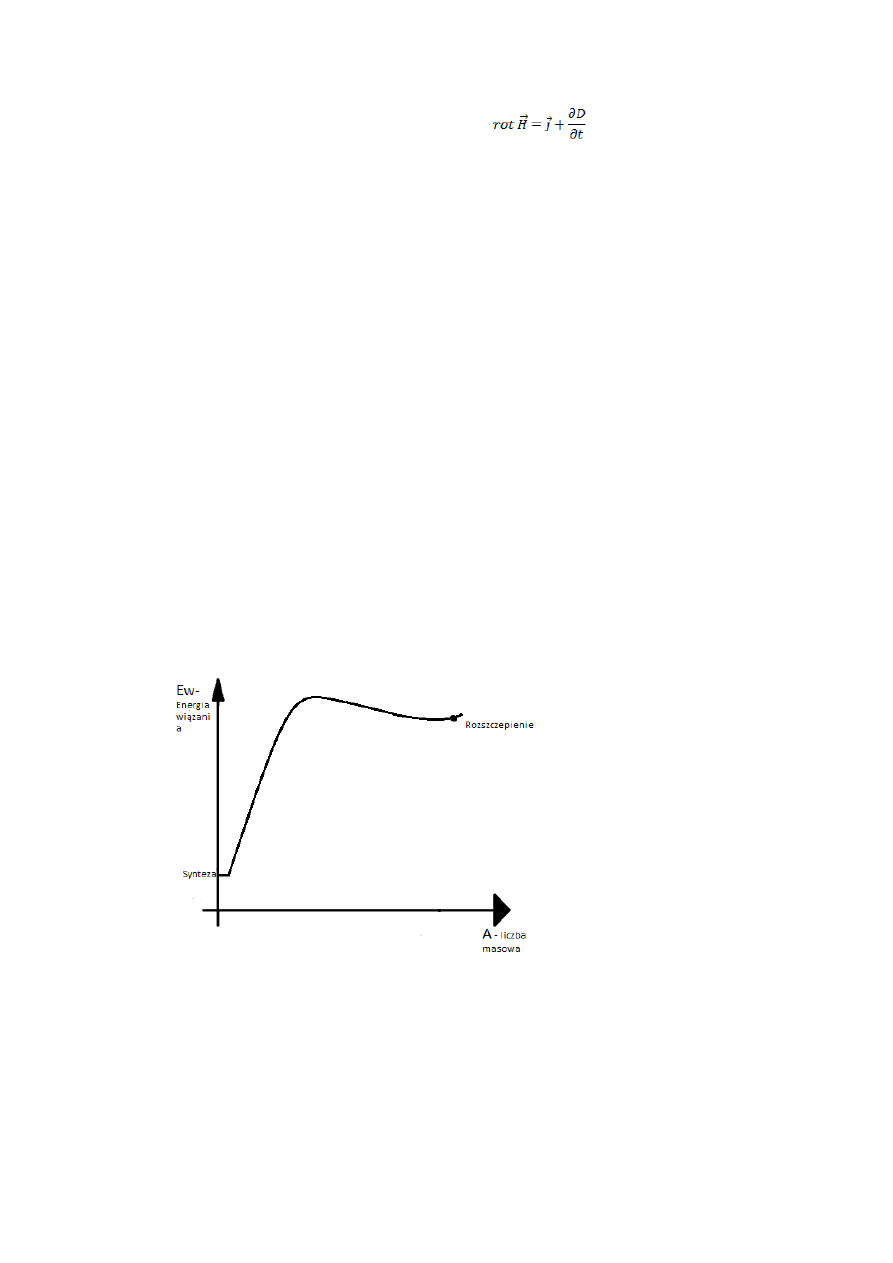
Prawo Ampere’a rozszerzone przez Maxwella:

Wiry pola magnetycznego powstają w miejscach w których płynie prąd elektryczny, lub w
miejscach w których następuje zmiana w czasie indukcji pola elektrycznego.

29. A - liczba masowa(liczba nukleonów)

Z - liczba porządkowa(liczba protonów w jadrze)
Nukleon-suma liczbowa protonów i neutronów

30. Co wiąże ze sobą neutrony?

Siła Columba

31. Siły odziaływania międzycząsteczkowego (pomiędzy nukleonami)?

Grawitacyjnego
elektromagnetycznego
(Siły Jądrowe(Lekkie i Silne))

32. Energia wiązania - Energia potrzebna do wyrwania nukleonu z jadra atomu.

Praca jaką należy wykonać, aby wyrwać nukleon z jądra (ze studni potencjału).

33. Defekt masy jądra

Niedobór masy w jądrze atomu. Suma mas nukleonów swobodnych jest większa od
masy jadra atomu utworzonego przez te nukleony.

𝐸 = 𝛥𝑚𝑐

2

𝛥𝑚 – niedobór masy

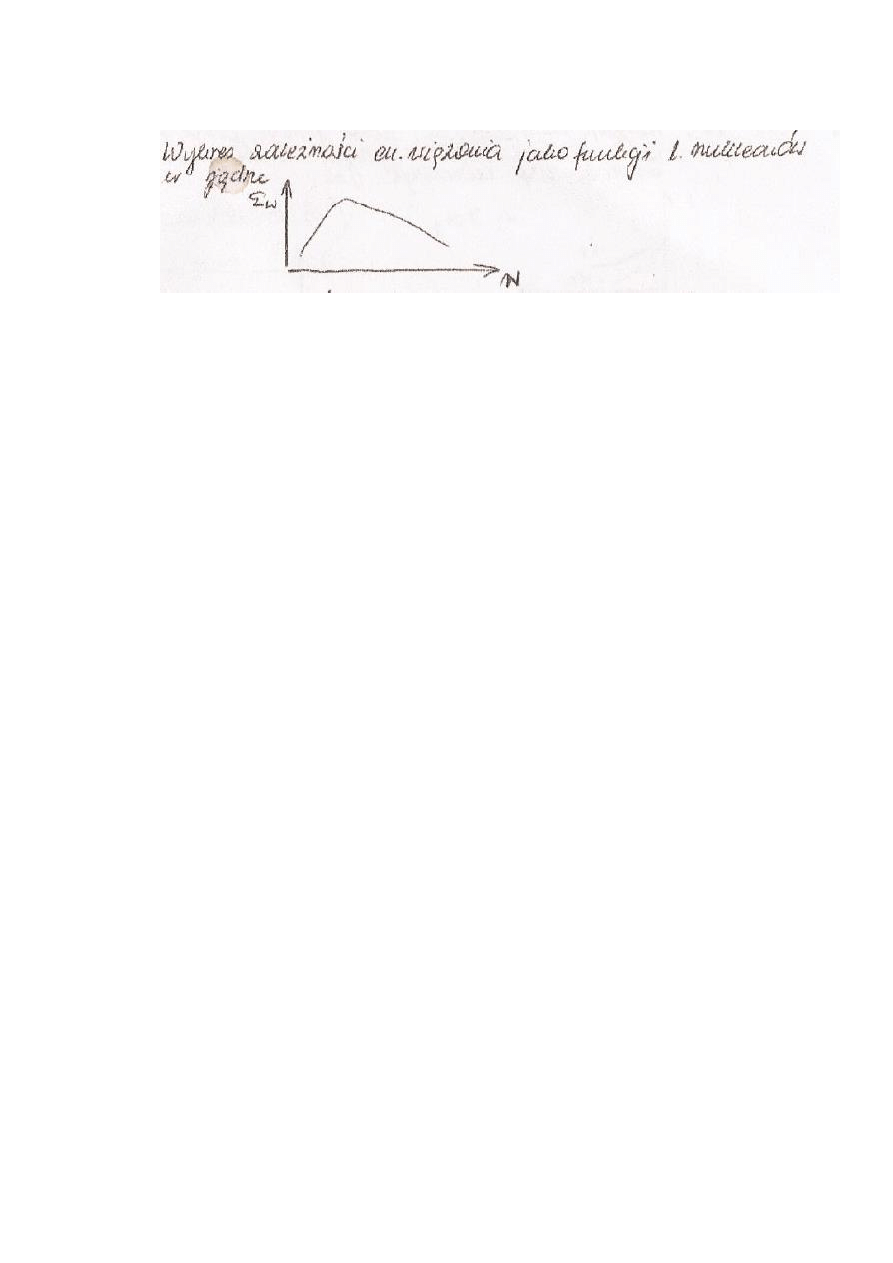
34. Zależność energii wiązania nukleonów w funkcji liczby nukleonów i protonów

Energia wiązania.

35. Temperatura jest miara energii kinetycznej ruchu cząsteczek.

Aby pokonać siłę Columba 2 protonów należy albo odpowiednio
przyspieszyć(poprzez akcelerator) albo użyć bardzo wysokiej temperatury.

36.

37. Równanie jądrowe cząstki β-

A

A

X -> Y + e- + v

A - liczba masowa

Z

Z+1

Z - liczba porządkowa

v-neutrino

38. Równanie jądrowe cząstki β+

e- elektron

A

A

e+ pozyton

X -> Y + e+ + v
Z

Z-1

39. Równanie jądrowe cząstki α

A A-4

4

X -> Y + α
Z Z-2

2

40. Anihilacja-połączenie materii i antymaterii, pozostaje tylko energia.

e+ + e- -> hv

E=h*v

Gdzie

E-energia

h-stała planca

v-częstotliwość drgań światła