3

Całka krzywoliniowa nieskierowana

(całka krzywoliniowa funkcji skalarnej)

Niech

K – krzywa regularna w R

3

f – pole skalarne, tzn

R

→

K

f :

)

(K

C

f

∈

Wtedy

•

krzywą K dzielimy na n części o długościach

,...,n

,

, i

∆s

i

2

1

=

•

w każdej z krzywych cząstkowych wybieramy po jednym punkcie

i

M

•

tworzymy sumę

∑

=

∆

⋅

=

n

i

i

i

n

s

M

f

1

)

(

σ

Definicja

Jeśli przy

∞

→

n

i

0

max

,...,

1



 →



∆

∞

→

=

n

i

n

i

s

istnieje granica

n

n

σ

∞

→

lim

niezależna od sposobu

podziału krzywej i od wyboru punktu

M

i

, to granicę tę nazywamy

całką krzywoliniową

nieskierowaną i oznaczamy

∫

K

fds .

Uwaga

Gdy zmienimy zwrot krzywej na przeciwny przy tym samym podziale krzywej i tych samych
wybranych punktach, to nie zmienią się sumy

n

σ

, a zatem nie zmieni się całka

krzywoliniowa nieskierowana

∫

∫

=

−

K

K

fds

fds

.

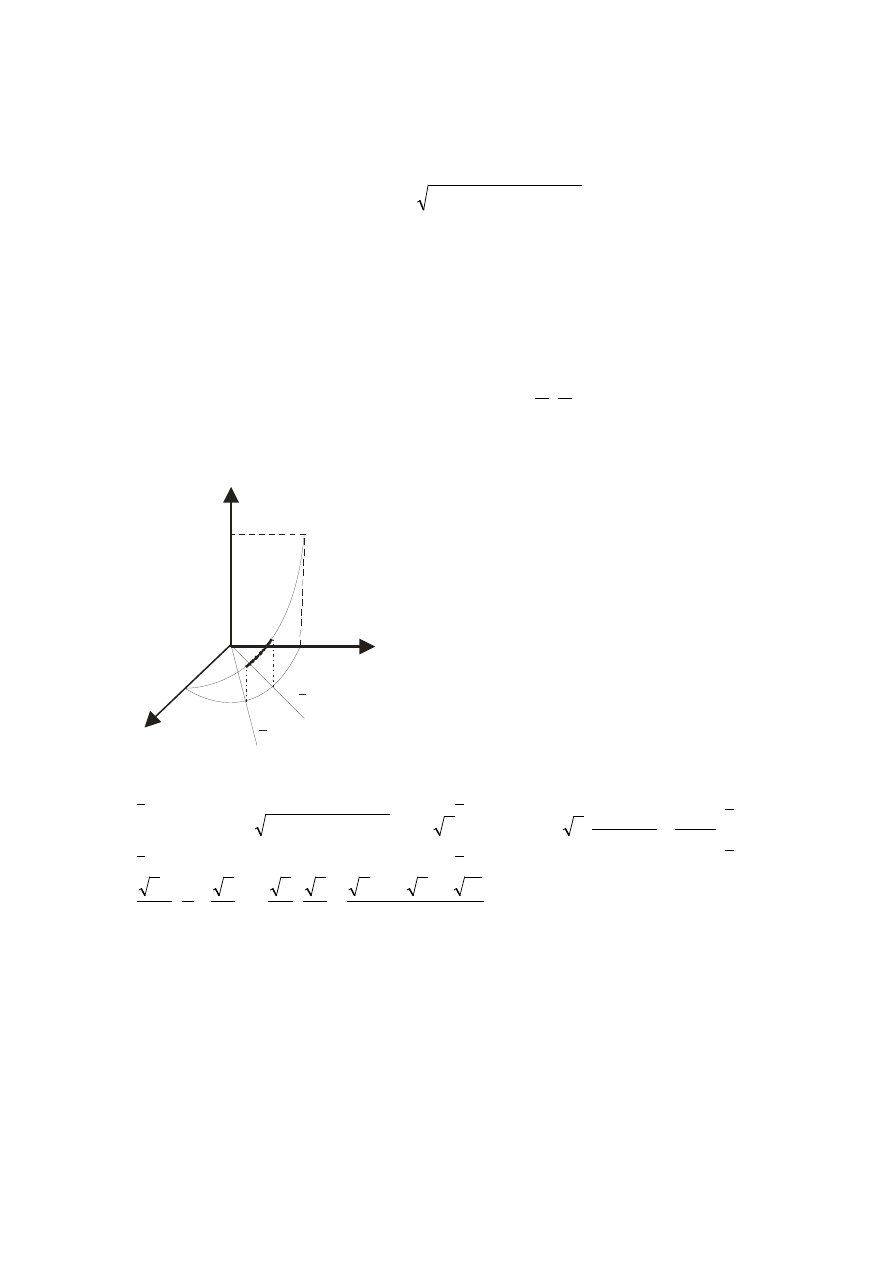
x

y

r

( )

α

r

( )

β

∆

s

M

z

i

i

4

Twierdzenie (o zamianie całki krzywoliniowej nieskierowanej na całkę oznaczoną)

Jeżeli

K – krzywa regularna oraz

)

(

K

C

f

∈

,

to

∫

∫

+

+

⋅

=

K

dt

t

z

t

y

t

x

t

z

t

y

t

x

f

ds

z

y

x

f

β

α

)

(

)

(

)

(

))

(

),

(

),

(

(

)

,

,

(

2

'

2

'

2

'

.

Przykład

Obliczyć całkę

∫

=

K

xyzds

I

2

, gdzie

K:











=

=

=

t

z

t

y

t

x

2

sin

cos

dla









∈

4

,

6

π

π

t

.

Oczywiście krzywa

K jest regularna oraz

)

(

K

C

f

∈

. Zatem można zastosować twierdzenie o

zamianie całki krzywoliniowej na całkę oznaczoną.

2

)

(

cos

)

(

sin

)

(

'

'

'

=

=

−

=

t

z

t

t

y

t

t

x

Stąd

12

15

3

5

6

5

2

3

2

5

1

2

5

2

1

6

5

4

2

sin

2

2

cos

5

2

2

sin

5

2

4

cos

sin

2

sin

cos

2

4

6

4

6

4

6

2

2

−

+

=

⋅

−

⋅

+

⋅

=

=









+

−

=

⋅

=

+

+

⋅

⋅

=

∫

∫

π

π

π

π

π

π

π

π

t

t

t

tdt

t

dt

t

t

t

t

t

I

x

y

z

1

1

π

π

π

6

4

K

5

Uwaga

1. Jeśli krzywa K leży w płaszczyźnie OXY,

OXY

K

⊂

,







=

=

)

(

)

(

:

t

y

y

t

x

x

K

, gdzie

]

,

[

β

α

∈

t

oraz

)

(K

C

f

∈

,

to

(

)

dt

t

y

t

x

t

y

t

x

f

ds

y

x

f

K

)

(

)

(

)

(

),

(

)

,

(

2

2

+

=

∫

∫

β

α

.

2. Jeśli krzywa K leż w płaszczyźnie OXY i zadana jest w sposób jawny, tzn.

],

,

[

dla

)

(

b

a

x

x

y

y

∈

=

to K możemy sparametryzować:

K:

1

]

,

[

gdzie

,

)

(

'

'

'









=

=

⇒

∈







=

=

y

y

x

b

a

x

x

y

y

x

x

i wtedy

(

)

.

)

(

1

)

(

,

)

,

(

2

'

dx

x

y

x

y

x

f

ds

y

x

f

b

a

K

+

⋅

=

∫

∫

Przykład

Obliczyć

∫

K

yds

x

2

, gdzie

4

:

2

2

=

+

y

x

K

,

0

≥

y

.

Funkcja

2

4

x

y

−

=

dla

[

]

2

,

2

−

∈

x

określa krzywą K.

Obliczamy

2

'

4

x

x

y

−

−

=

i korzystamy z uwagi 2.

3

32

3

2

2

4

1

4

2

2

3

2

2

2

2

2

2

2

2

2

=

=

=

−

+

⋅

−

=

+

−

−

−

∫

∫

x

dx

x

dx

x

x

x

x

I

6

Interpretacja geometryczna całki krzywoliniowej niekierowanej

1. Niech

1

≡

f

na K.

Wtedy

∫

=

K

K

ds

- długość krzywej K.

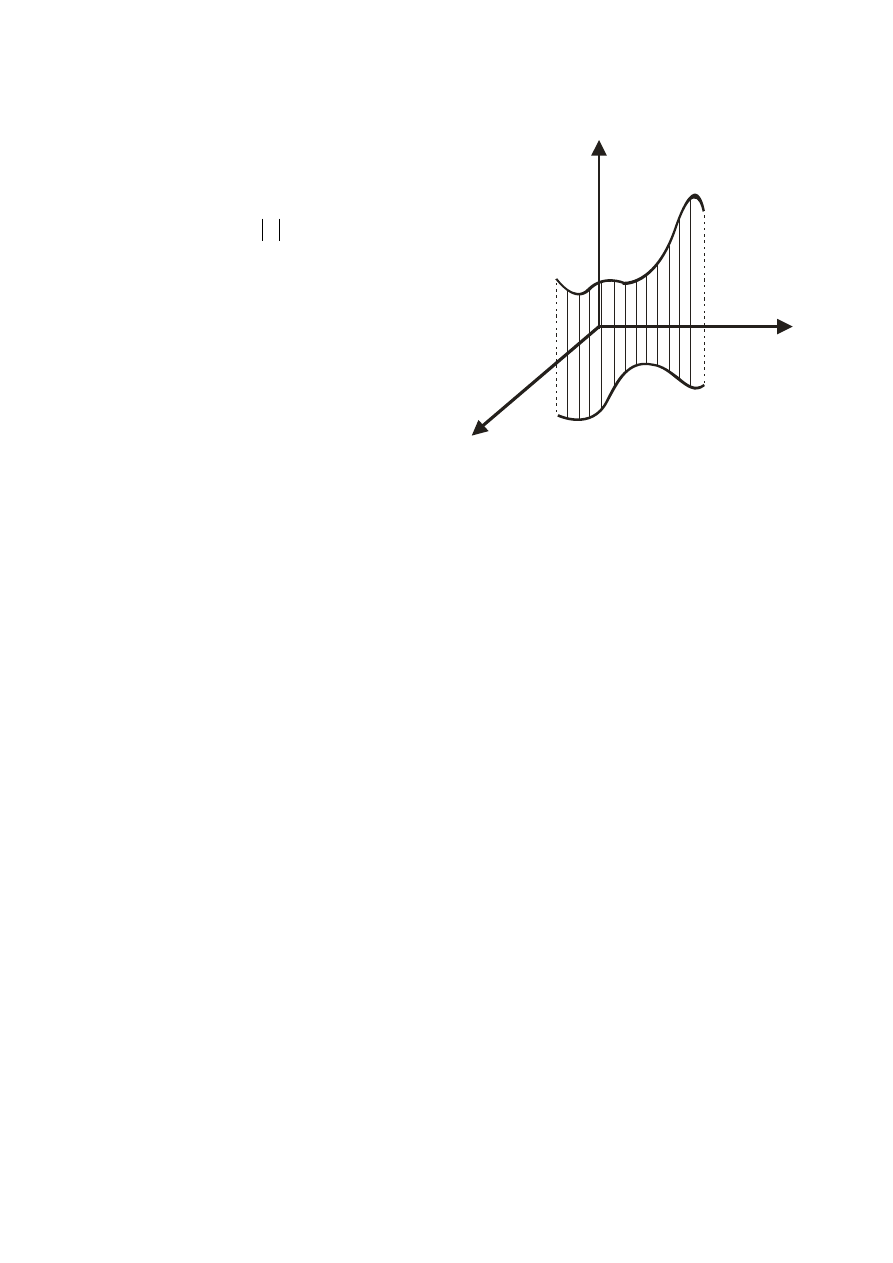
2. Niech K – krzywa płaska,

,

OXY

K

⊂

.

0

),

(

>

∈

f

K

C

f

Wtedy

∫

K

ds

y

x

f

)

,

(

- pole części

powierzchni walcowej znajdujące się pod wykresem funkcji

f.

Interpretacja fizyczna całki krzywoliniowej nieskierowanej

1. Jeśli

ρ

- gęstość liniowa masy rozmieszczonej wzdłuż krzywej

K, to

∫

K

ds

ρ

- masa krzywej

K

2. Jeśli

d – funkcja określającą odległość punktu krzywej K od pewnej prostej, to

∫

K

ds

d

ρ

2

- moment bezwładności krzywej

K względem tej prostej.

Uwaga

Niech

n

K

K

K

K

...

2

1

∪

∪

=

, gdzie

i

K krzywa regularna dla i=1,…,n.

Wtedy definiujemy

∑ ∫

∫

=

=

n

i

K

K

i

fds

fds

1

:

.

x

y

z

z=f(x,y)

K