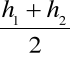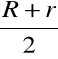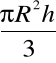STEREOMETRIA

STEREOMETRIA - geometria w przestrzeni

BRYŁA - figura w przestrzeni, musi spełniać następujące warunki: musi być ograniczona; musi być domknięta ( czyli zawierać swój brzeg ); do każdej kuli, której środek należy do tej figury, musi należeć ( co najmniej jeden ) punkt wewnętrzny tej figury; każde dwa punkty tej figury można połączyć linią łamaną w niej zawartą.

Bryłami nie są figury składające się ze skończonej liczby punktów, linie, powierzchnie, itp.

Jeżeli dwie bryły mają ( co najmniej jeden ) punkt wspólny to ich suma też jest bryłą

KLASYFIKACJA FIGUR PRZESTRZENNYCH

1. BRYŁY OBROTWE - powstają w wyniku obrotu figury f dookoła osi l

• Kula - bryła powstała przez obrót koła wokół prostej zawierającej średnicę tego koła

• Walec - bryła powstała przez obrót prostokąta dookoła prostej zawierającej jeden z boków

• Stożek - bryła powstała w wyniku obrotu trójkąta prostokątnego dookoła prostej zawierającej jedną z przyprostokątnych

• Stożek ścięty - bryła powstała w wyniku obrotu trapezu prostokątnego dookoła prostej zawierającej bok prostopadły do obu podstaw

2. WIELOŚCIANY - bryły, które są iloczynem półprzestrzeni

W wielościanie wyróżniamy: krawędzie, wierzchołki, ściany boczne, które są wielokątami

TWIERDZENIE EULERA: W+S-2=K W - liczba wierzchołków S - liczba ścian K - liczba krawędzi np. sześcian: 8+6-2=12 czworościan: 4+4-2=6

• Wielościany foremne - wielościany wypukłe, w których wszystkie ściany są wielokątami foremnymi o tej samej liczbie boków i wszystkie wypukłe kąty dwuścienne wyznaczone przez sąsiednie ściany mają równe miary

1.Czworościan

2.Sześcian

3.Ośmiościan

4.Dwunastościan

5.Dwudziestościan

Nazwa wielościanu foremnego	Rodzaj ściany	Liczba
		Wierzchołków	Krawędzi	Ścian	Ścian schodzących się w wierzchołku
Czworościan	trójkąt	4	6	4	3
Sześcian	czworokąt	8	12	6	3
Ośmiościan	trójkąt	6	12	8	4
Dwunastościan	pięciokąt	20	30	12	3
Dwudziestościan	trójkąt	12	30	20	5

• Graniastosłupy - wielościany, w których dwie ściany boczne są wielokątami przystającymi, leżącymi w płaszczyznach równoległych, a krawędzie boczne są do siebie równoległe.

Dwa przystające wielokąty nazywamy podstawami graniastosłupa, a równoległoboki ścianami bocznymi. Ściany boczne tworzą pobocznicę graniastosłupa, ich wspólne boki - krawędzie boczne, a boki wielokątów podstawy - krawędzie podstawy. Odległość płaszczyzn obu podstaw nazywamy wysokością graniastosłupa.

1.Graniastosłupy proste - graniastosłupy, których krawędzie boczne są prostopadłe do podstaw np. sześcian, prostopadłościan

2.Graniastosłupy prawidłowe - graniastosłupy proste, których podstawa jest wielokątem foremnym

• Ostrosłupy - wielościany utworzone z wielokąta płaskiego i z trójkątów o wspólnym wierzchołku.

Wielokąt płaski nazywamy podstawą ostrosłupa, a trójkąty ścianami bocznymi. Ściany boczne tworzą pobocznicę ostrosłupa, ich wspólne boki - krawędzie boczne, a boki wielokąta podstawy - krawędzie podstawy. Punkt wspólny dla wszystkich ścian bocznych nazywamy wierzchołkiem ostrosłupa, a jego odległość od płaszczyzny podstawy - wysokością ostrosłupa.

1.Ostrosłup prosty - ostrosłup, którego krawędzie boczne są równej długości ( rzut prostokątny wierzchołka ostrosłupa na płaszczyznę podstawy jest środkiem okręgu opisanego na wielokącie podstawy ).

2.Ostrosłup prawidłowy - ostrosłup prosty, którego podstawa jest wielokątem foremnym.

• TWIERDZENIE I: Wszystkie krawędzie boczne ostrosłupa prawidłowego są jednakowej długości i tworzą jednakowe kąty z płaszczyzną podstawy.

WNIOSEK: Ściany boczne ostrosłupa prawidłowego są przystającymi trójkątami równoramiennymi.

• TWIERDZENIE II: Jeżeli podstawą ostrosłupa jest wielokąt foremny i wszystkie krawędzie boczne mają równe długości, to ostrosłup jest prawidłowy.

• TWIERDZENIE III: Jeżeli podstawą ostrosłupa jest wielokąt foremny i wszystkie krawędzie boczne ostrosłupa tworzą z płaszczyzną podstawy równe kąty, to ostrosłup jest prawidłowy.

• TWIERDZENIE IV: Następujące warunki są równoważne:

1. Wszystkie krawędzie boczne ostrosłupa mają równe długości;

2. Wszystkie krawędzie boczne ostrosłupa tworzą równe kąty z płaszczyzną podstawy;

3. Na podstawie ostrosłupa możemy opisać okrąg, którego środkiem jest spodek wysokości ostrosłupa.

WZORY NA POWIERZCHNIE I OBJĘTOŚCI BRYŁ

L.p.	Nazwa figury	Powierzchnia [P]	Objętość [V]
1	Sześcian	Całkowita: P = 6a^2 A- dł. krawędzi	V = a^3
2	Prostopadłościan	Całkowita: P = 2 (ab+ac+bc) a, b, c- dł. krawędzi	V = a b c
3	Graniastosłup o podstawach równoległych	Całkowita: P = 2G + S l G- pole podstawy S- obwód przekroju prostopadłego do krawędzi l- krawędź	V = G h h- wysokość
4	Graniastosłup trójkątny ukośnie ścięty	Całkowita: P = G1 + G2 + Pb G1, G2 - pola podstaw Pb- powierzchnia boczna	V = G G- pole przekroju poprzecznego prostopadłego do krawędzi a, b, c- długości równoległych krawędzi
5	Ostrosłup całkowity	Całkowita: P = G + Pb G- pole podstawy Pb- powierzchnia boczna	V = G h h- wysokość
6	Ostrosłup prosto ścięty	Całkowita: P = G1 + G2 + Pb G1, G2-pola podstaw Pb- powierzchnia boczna	V = (G1 + + G2) h- wysokość
7	Walec obrotowy	Boczna: P1 = 2πRh Całkowita: P = 2πR (h + R) R- promień podstawy walca (koła) h- wysokość walca	V = π R^2h
8	Walec obrotowy ukośnie ścięty	Boczna: P1 = πR (h1+h2) R- promień podstawy walca (koła) h1- najmniejsza tworząca h2- największa tworząca	V = πR^2
9	Walec obrotowy wydrążony (rura)	Boczna zewn. i wewn.: P1 = 2πh (R+r) Całkowita: P = 2πh (R+r)+2π (R^2-r^2) = = 2π (R+r) (h+R-r) h- wysokość walca R- promień zewnętrzny r- promień wewnętrzny	V = πh (R^2-r^2) = = πhb (2R-b) = = πhb (2r+b) = = 2πhbq b- grubość ścianki q- średni promień q =
10	Stożek obrotowy całkowity	Boczna: P1 = π R l = πR Całkowita: P = πR (R+l) R- promień podstawy stożka h- wysokość stożka l- tworząca stożka	V = = 1,047 R^2h
11	Stożek obrotowy prosto ścięty	Boczna: P1 = πl (R+r) Całkowita: P = πR (R+l) + πr (r+l) R- promień podstawy stożka (koła) o większej powierzchni r- promień podstawy stożka (koła) o mniejszej powierzchni l- tworząca stożka	V = π (R^2 + Rr + r^2)
12	Kula pełna	P = 4πR^2 R- promień kuli	V = π R^3 4,189 R^3

Opracowała: Hanna Jakubowska

Klasa IV a

---