Zadanie 19:

Wzór na sumę n początkowych wyrazów ciągu geometrycznego.

, gdy
[A]

zaś
, gdy
[B]

Wzór [B] jest oczywisty, gdyż jeżeli
, to
dla każdego n, więc

Dowód (indukcyjny) wzoru [A].

Dla n=2 wzór jest prawdziwy, ponieważ

Załóżmy, że wzór [A] jest prawdziwy dla liczby naturalnej n (
, gdy ciąg jest k-wyrazowy} i rozważmy sumę
:

Podstawmy

n+1 = k

a wtedy

QED

Przykład 1:

W ciągu geometrycznym

oraz q = 2.

Obliczyć sumę dziesięciu początkowych wyrazów tego ciągu.

Rozwiązanie:

Wystarczy skorzystać z wzoru [A]:

Odp. 2046.

Przykład 2:

Udowodnić, że suma odwrotności wszystkich wyrazów skończonego ciągu geometrycznego równa jest sumie wszystkich jego wyrazów podzielonej przez iloczyn pierwszego i ostatniego wyrazu.

Rozwiązania:

Rozważmy ciąg geometryczny

Obliczmy sumę odwrotności wyrazów tego ciągu

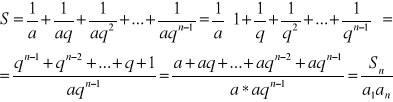
QED

Przykład 3:

Każdy wyraz ciągu geometrycznego (z wyjątkiem pierwszego i ostatniego, gdy ciąg jest skończony) spełnia warunek

[B]

Istotnie, ponieważ

oraz

więc

QED

Jeżeli wyrazy ciągu geometrycznego są dodatnie, to z równości [B] wynika równość:

---