Liczby zespolone i ich interpretacja geometryczna

Liczbą zespoloną nazywamy parę uporządkowaną liczb rzeczywistych (a,b).

Często taką parę zapisuje się w postaci sumy

z = a + bi, gdzie i²=-1

Tę postać liczby zespolonej nazywamy postacią kanoniczną.

Liczbę (rzeczywistą) a nazywamy częścią rzeczywistą, zaś liczbę b częścią urojoną liczby zespolonej z.

Część rzeczywistą oznaczamy Re z, a część urojoną symbolem Im z, mamy więc:

Re z = a

Im z = b

Liczby zespolone postaci a+0i zapisujemy jako a i utożsamiamy z liczbami rzeczywistymi.

Liczba zespolona jest równa zero, wtedy i tylko wtedy, gdy

Re z = 0 i Im z = 0

Zauważmy również, że kolejność liter w zapisie z=a+bi nie gra roli:

a + bi = a + ib = bi + a = ib + a

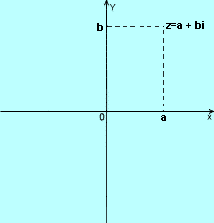
Liczby zespolone interpretujemy geometrycznie jako punkty płaszczyzny.

Liczbie zespolonej a+bi odpowiada punkt o współrzędnych (a,b) płaszczyzny zaopatrzonej w prostokątny układ współrzędnych.

Punktom osi OX odpowiadają liczby rzeczywiste.

Płaszczyznę, na której umieściliśmy liczby zespolone, nazywamy płaszczyzną Gaussa.

Liczbą przeciwną do z=a+bi nazywamy -z=-a-bi,

_

Natomiast liczbę z=a-bi nazywamy liczbą sprzężoną do z lub sprzężeniem liczby z.

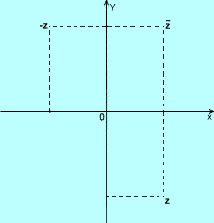
Zauważmy, że podwójne sprzężenie liczby z jest równe dokładnie liczbie z.

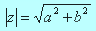
Natomiast modułem liczby zespolonej z=a+bi nazywamy

Istniej pewien związek między modułem liczby z a jej

_

sprzężeniem z

Działania na liczbach zespolonych

Niech teraz

Liczby zespolone są równe, gdy mają jednakowe zarówno części rzeczywiste i części urojone:

Dodajemy, odejmujemy i mnożymy liczby zespolone tak, jak wyrażenia algebraiczne pamiętając, że i²=-1.

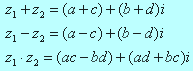
Tak więc:

Trochę trudniej jest z dzieleniem, a dokładniej do doprowadzenia ilorazu do postaci Re z + Im z i.

Zastosujemy tu wzór:

Obliczmy teraz iloraz

oczywiście zakładając, że z2≠0

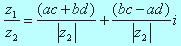
Działania arytmetyczne na liczbach zespolonych są rozszerzeniem działań na liczbach rzeczywistych, tzn. w przypadku liczb rzeczywistych jest obojętne czy np. mnożymy je jako liczby rzeczywiste czy zespolone z częścią urojoną równą zero.

(Powyższe wzory można przyjąć za definicję działań.)

Wynika z nich, że działania dodawania i mnożenia liczb zespolonych są łączne i  przemienne oraz mnożenie jest rozdzielne względem dodawania.

Zachowane są również znane własności odejmowania i dzielenia.

Powyższe stwierdzenia powodują, że dla liczb zespolonych prawdziwe są wzory:

• skróconego mnożenia,

• dwumianowy Newtona,

• twierdzenie Bezout itd.

Nie określamy natomiast nierówności liczb zespolonych innych niż rzeczywiste. Mówiąc więc, że liczba jest dodatnia nie musimy dodawać, że jest ona rzeczywista.

Postać trygonometryczna liczby zespolonej

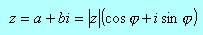
Liczbę zespoloną możemy przedstawić w postaci trygonometrycznej:

gdzie

Liczbę |z| nazywamy modułem z, a kąt skierowany ϕ (dokładniej jego miarę) argumentem liczby z≠0 i oznaczamy arg z.

Wartość argumentu liczby z czyli ϕ określamy na podstawie wartości funkcji cosinus i sinus dla ϕ, które są dane wzorami:

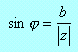
i

Ta postać liczby zespolonej ma interpretację geometryczną:

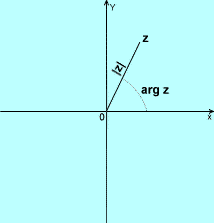
Wygodniej jest nie ograniczać zakresu zmienności argumentu ϕ , ale tracimy przez to jednoznaczność.

Liczbie zespolonej różnej od zera odpowiada nieskończenie wiele argumentów.

Jeżeli ϕ jest argumentem liczby z, to każdy inny argument tej liczby wyraża się wzorem

gdzie k jest liczbą całkowitą.

Dwie liczby zespolone są sobie równe, wtedy i tylko, gdy mają równe moduły i argumenty różniące się o całkowitą wielokrotność liczby 2Π. Jeżeli ϕ∈[0,2Π] to nazywamy argumentem głównym i oznaczamy Arg z.

(Niektóre podręczniki nieco inaczej definiują argument główny: Argumentem głównym nazywają ϕ, gdy ϕ∈(−Π,Π]).

Trygonometryczna postać liczby zespolonej bardzo ułatwia mnożenie i dzielenie, natomiast niezbyt nadaje się do dodawania i odejmowania.

Jeżeli

i

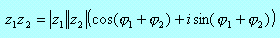
to

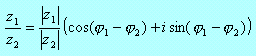
gdzie z₂≠0.

Potęga i pierwiastek z liczby zespolonej

Postać trygonometryczna liczby zespolonej jest również wykorzystywana do liczenia potęg i pierwiastków liczb zespolonych.

Gdy weźmiemy wzór na mnożenie liczb zespolonych w postaci trygonometrycznej dla z₁=z₂ i rozszerzymy na dowolną ilość liczb zespolonych, to otrzymamy wzór na n-tą potęgę liczby zespolonej zwany wzorem Moivre'a:

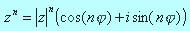
Natomiast pierwiastki z liczby zespolonej są dane wzorem:

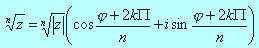
gdzie

Zauważmy, że liczba różnych pierwiastków liczby z jest równa dokładnie stopniowi pierwiastka, który liczymy.

Są to pierwiastki dla k=0,1...,n-1.

Możemy liczyć wartości pierwiastków dla innych całkowitych k, ale otrzymamy wtedy wartości, które już wyliczyliśmy dla k=0,1...,n-1.

Jeżeli się przyglądniemy wartościom pierwiastków liczby zespolonej, to zauważymy, że ich moduły są takie same i argumenty różnią się o wielokrotność

Z tej obserwacji wnioskujemy, że pierwiastki leżą na jednym okręgu o środku w punkcie 0 i promieniu równym modułowi pierwiastka oraz że pierwiastki dzielą okręg na n równych części.

Jest to bardzo użyteczny wniosek przy zaznaczaniu pierwiastków na płaszczyźnie Gaussa, ponieważ wystarczy narysować okręg o promieniu

policzyć i zaznaczyć jeden pierwiastek danej liczby oraz podzielić okrąg na n równych części tak, aby policzony pierwiastek był jednym z punktów podziału. W ten sposób otrzymujemy wszystkie pierwiastki liczby z.

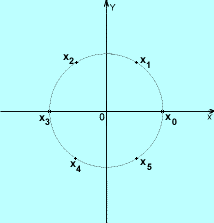
Pierwiastki szóstego stopnia z 1 - x₀ ... x₅.

---