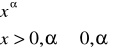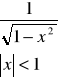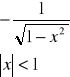Pochodne funkcji elementarnych
c-stała |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pochodna funkcji danej w postaci parametrycznej.
Dane są funkcje ![]()
, ![]()
określone i ciągłe względem parametru ![]()
podając związek zmiennej niezależnej ![]()
za zmienną zależną ![]()
.
Zakładamy, że
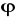
jest ściśle monotonicznaIstnieje skończona pochodna
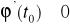
Zatem istnieje funkcja odwrotna ![]()
funkcja ta jest ciągła i ściśle monotoniczna
Funkcja złożona ![]()
jest ciągła.
Ponieważ ![]()
![]()
gdzie ![]()
więc na podstawie twierdzenia o pochodnej funkcji złożonej otrzymujemy
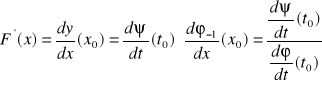
czyli 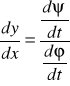
Wyszukiwarka
Podobne podstrony:
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
więcej podobnych podstron