Całka nieoznaczona - definicje, własności

W rachunku różniczkowym dla danej funkcji f(x) wyznaczało się f `(x). W rachunku całkowym wyznaczamy funkcję F(x), dla której znamy F'(x) tzn. wiadomo, że F'(x) = f(x), gdzie dane mamy f(x), a znaleźć należy F(x)

Definicja 1 funkcja pierwotna:

Funkcję pierwotną danej funkcji rzeczywistej f(x) w przedziale (a,b) nazywamy taką funkcję F(x), która ma własność:

F'(x) = f(x) dla

Przykład:

f(x) = cosx

ma funkcję pierwotną F(x) = sinx gdzie

bo F'(x) = cosx = f(x) dla

Twierdzenie 1:

Jeżeli f(x) ma w przedziale (a,b) funkcję pierwotną F(x) to f(x) ma w tym przedziale nieskończenie wiele tych funkcji pierwotnych. Każda z nich ma postać:

G(x) = F(x) + C, gdzie C jest dowolną stałą

Dowód:

W dowodzie wykażemy, że:

• Dla danej funkcji pierwotnej F(x) funkcja G(x) = F(x) +C, C = const, jest funkcją pierwotną funkcji f(x)

• Każdą funkcję pierwotną H(x) funkcji f(x) można uzależnić od tej danej F(x) i ta zależność ma postać H(x) = F(x) + C, gdzie C = const

dot. pierwszego:

Z założenia twierdzenia wiadomo, że F(x) jest funkcją pierwotną dla f(x) w przedziale (a,b) tzn. F'(x) = f(x) w (a,b).

Weźmy G(x) = F(x) + C, C = const.

Wówczas G'(x) = [F(x) + C]' = F'(x) = f(x) dla

Czyli G(x) spełnia warunki definicji funkcji pierwotnej dla f(x)

dot. drugiego:

Weźmy dwie funkcje pierwotne dla f(x) w przedziale (a,b) daną F(x) i inna H(x)

tzn F'(x) = f(x) dla
H'(x) = f(x) dla

Zatem F'(x) - H'(x) = 0 dla

Zatem [F(x) - H(x)]' = 0 dla

Więc F(x) - H(x) + C, C = const

Czyli H(x) = F(x) +
, gdzie
= C (
- stałą dowolna)

Tzn. każdą funkcję pierwotną H(x) funkcji f(x) można przedstawić w postaci F(x) + C, C = const, a F(x) jest wyróżnioną funkcją pierwotną.

Definicja 2 całka nieoznaczona

Całką nieoznaczoną danej funkcji f(x) w przedziale (a,b) nazywamy najogólniej zapisaną jej funkcję pierwotną.

Całkę nioznaczoną zapisujemy symbolem

Zatem
= F(x) + C, gdzie F(x) jest funkcją pierwotną funkcji f(x), czyli F'(x) = f(x) dla
zaś C - dowolna stała

= F(x) +C
F'(x) = f(x) , C=const

UWAGA! F(x) + C, C = const przedstawia rodzinę funkcji

Twierdzenie 2:

Każda funkcja f(x) ciągła w przedziale (a,b) ma swoją funkcję pierwotną F(x) a więc ma swoją całkę nieoznaczoną w przedziale (a,b)

Wzory podstawowe:

1. 
   

2. 
   

3. 
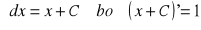
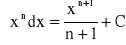
   dla dowolnej liczby rzeczywistej n
   -1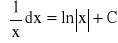

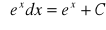
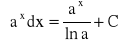
4. 
   

5. 
   

6. 
   dla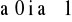
   

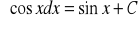
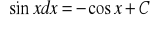
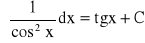
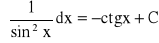
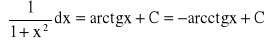
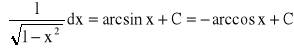
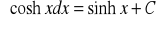
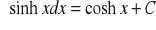
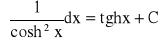
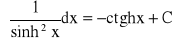
7. 
   

8. 
   

9. 
   

10. 
    

11. 
    

12. 
    

13. 
    

14. 
    

15. 
    

16. 
    

Własności całki nieoznaczonej:

1. Jeżeli istnieje całka
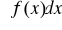
   , to (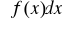
   )' = f(x)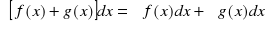

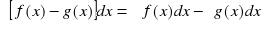
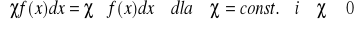
2. 
   

3. 
   

4. 
   

Metody obliczania całek nieoznaczonych:

1. Metoda bezpośredniego całkowania oparta jest na wzorach podstawowych, własnościach a, b, c, d i na przekształceniach algebraicznych.

np.:

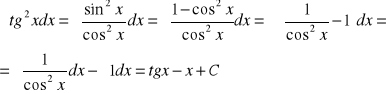
2. Metoda całkowania przez podstawienie opisana jest w twierdzeniu:

Twierdzenie 3:

Jeżeli spełnione są warunki:

1. funkcja f(x) jest ciągła w przedziale (a,b)

2. funkcja x = (t) jest określona i ciągła w przedziale (, oraz dla t
   (, wartości funkcji x są takie, że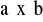
   

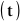
3. ('
   jest funkcją ciągłą dla t
   
   

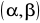
to zachodzi równość, zwana wzorem na całkowanie przez podstawienie:

Powyższy wzór pokazuje jak zmienia się całka
przy podstawieniu x = (t)

Dowód:

Z I wynika, że całka
istnieje.

Zatem według definicji całk nieoznaczonej:

F'(x) = f(x)

Dla F(x) można według II i III utworzyć funkcję złożoną F((t))

Ta funkcja ma pochodną:

Uwzględniając to, że:

mamy:

czyli:

Definicja całki mówi, że
i że

Równość:
oznacza zatem:

Ale

Ostatecznie:

Czyli:

UWAGA! Wzór o podstawianiu w całce wykorzystywany jest w następującej postaci:

 Metoda całkowania przez części opisana jest w twierdzeniu:

Twierdzenie 4:

Jeżeli funkcje u(x) i v(x) są funkcjami ciągłymi wraz z pochodnymi u'(x) i v'(x), to zachodzi równość zwana wzorem na całkowanie przez części:

Dowód:

Teza stanowi o wyniku całki

ale według definicji:

W celu dowiedzenia tezy twierdzenia 4 wystarczy pokazać, że pochodna prawej strony jest równa u(x)*v'(x)

Mamy więc:

(według własności a. całki)

Potwierdza to poprawność prawej strony we wzorze twierdzenia 4

---