Granica funkcji, ciągłość funkcji, definicje, twierdzenia

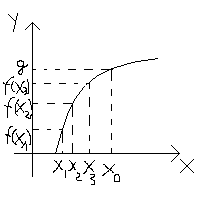
Definicja granicy funkcji w punkcie

Funkcja f musi być określona w pewnym sąsiedztwie punktu x₀

Definicja Heinego (ciągowa)

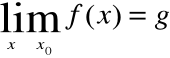
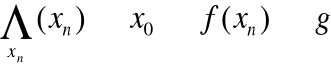
Mówimy, że funkcja f(x) posiada w x₀ granicę równą g jeżeli dla dowolnego ciągu argumentów zbieżnego do x₀ ciąg odpowiadających mu wartości jest zbieżny do niego

Jeżeli więc znajdziemy dwa ciągi argumentów zbieżne do x₀ , dla których ciągi odpowiadających im wartości są zbieżne do różnych liczb to oznacza, że funkcja x₀ nie posiada granicy.

Definicja Cauchy'ego (Epsilonowa)

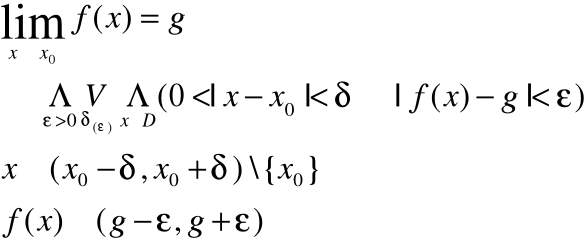
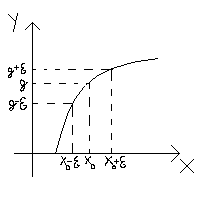
Definicja granicy jednostronnej funkcji w punkcie

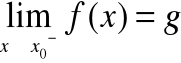
Lewostronna

1. definicją. Heinego

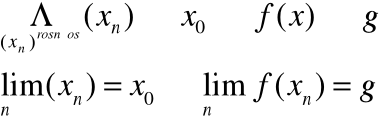
Mówimy, że funkcja f(x) posiada granicę lewostronną w punkcie jeżeli dla dowolnego ciągu argumentów rosnącego i zbieżnego do x₀ , ciąg odpowiadających mu wartości jest zbieżny do liczby g

2. 
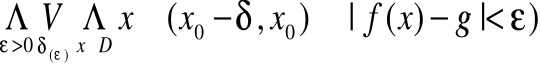
   definicją Cauchy'ego

Prawostronna

1. 
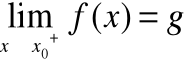
   definicją Heinego

2. 
   
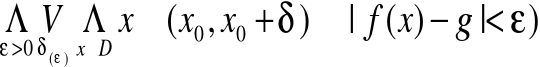
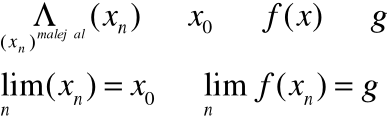
   definicją Cauchy'ego

Granice funkcji w nieskończoności

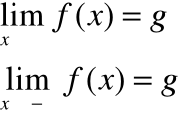
mówimy, że funkcja posiada w nieskończoności granicę równą g, jeżeli dla dowolnego ciągu argumentów rozbieżnych do nieskończoności ciąg odpowiadających im wartości jest zbieżny do g

1. 
   definicją Heinego

2. 
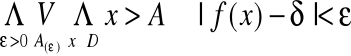
   definicją Cauchy'ego

Granica niewłaściwa

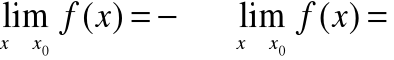
Mówimy, że funkcja f(x) posiada w punkcie x₀ granicę niewłaściwą równą +/-∞ jeżeli dla dowolnego ciągu argumentów zbieżnego do x₀ ciąg odpowiadających im wartości funkcji jest rozbieżny do +/-∞

1. definicją Heinego

2. 
   
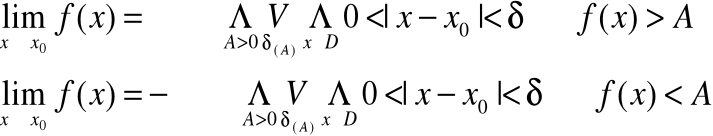
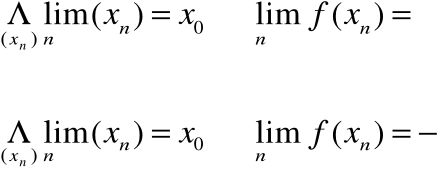
   definicją Cauchy'ego

Granica niewłaściwa w nieskończoności

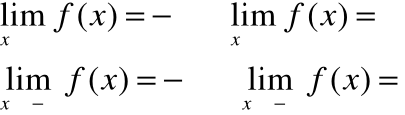
Mówimy, że funkcja f(x) posiada w +/-∞ granicę niewłaściwą równą +/-∞ jeżeli dla dowolnego ciągu argumentów rozbieżnego do +/-∞ ciąg odpowiadających im wartości funkcji jest rozbieżny do +/-∞

1. 
   definicją Heinego

i analogicznie reszta

2. definicją Cauchy'ego

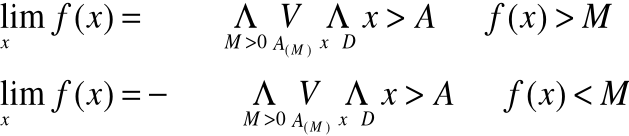
Właściwości z których korzystamy obliczając granice funkcji

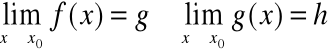
Jeżeli

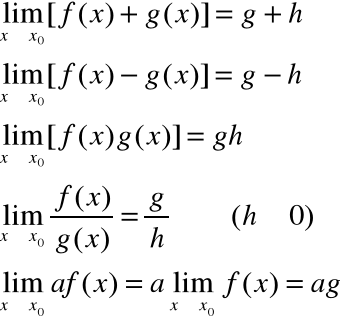
to prawdziwe są następujące wzory:

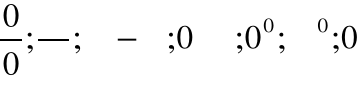
Symbole nieoznaczone

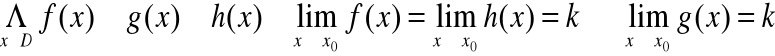
Twierdzenie o granicy trzech funkcji

Ciągłość funkcji

Mówimy, że funkcja jest ciągła w punkcie x₀ jeżeli:

1. Jest określona w punkcie x₀ , czyli posiada wartość

2. posiada granicę obustronną w punkcie x₀

3. granica funkcji jest równa wartości funkcji w tym punkcie

Funkcja jest ciągła w przedziale, jeżeli jest ciągła w każdym punkcie tego przedziału

Funkcje elementarne są ciągłe w swoich dziedzinach

Nieciągłość jest usuwalna gdy funkcja posiada granicę obustronną

Sebastian Kujath
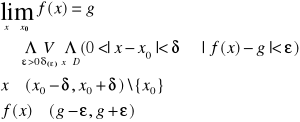
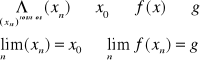
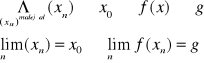
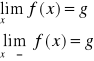
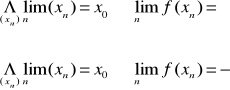
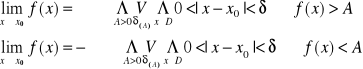
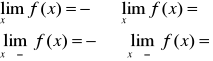
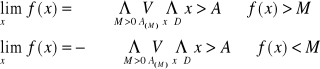
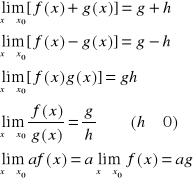