Zadanie 46

Indukcja matematyczna (zwana też indukcją zupełną) jest to metoda dowodzenia twierdzeń o liczbach naturalnych.

Niech T(n) oznacza formę zdaniową zmiennej n, określoną w dziedzinie N. Jeżeli w miejsce n podstawimy dowolną liczbę naturalną, to T(n) stanie się zdaniem prawdziwym albo fałszem, zależnie od wartości n. Jeżeli, na przykład T(n) oznacza wypowiedź: „n jest podzielne przez 3”, to T(6) jest zdaniem prawdziwym, natomiast T(7) jest zdaniem fałszywym. Jeżeli T(n) oznacza nierówność n < n², to T9n) jest zdaniem prawdziwym dla każdej liczby naturalnej większej od 1, natomiast zdanie T(1) jest fałszywe.

Zasada indukcji matematycznej:

Jeżeli:

1) istnieje taka liczba naturalna n₀, że T(n₀) jest zdaniem prawdziwym

2) dla każdej liczby naturalnej n > n₀ prawdziwa jest implikacja T(n) ⇒ T(n+1), to T(n) jest zdaniem prawdziwym dla każdej liczby naturalnej n > n₀

Dowód przeprowadzany metodą indukcji matematycznej nazywamy dowodem indukcyjnym; składa się on z dwóch etapów:

1. sprawdzenie, że T(n₀) jest prawdziwe,

2. dowodu, że dla każdego n > n₀, jeżeli T(n) jest prawdziwe, to T(n+1) jest prawdziwe.

Ten drugi etap nazywany krokiem indukcyjnym; zakładamy w nim, że dla liczby naturalnej n ≥ n₀ zdania T(n) jest prawdziwe (tzw. hipoteza indukcyjna) i na tej podstawie dowodzimy prawdziwości zdania T(n + 1).

Przykład 1:

Udowodnić, że dla każdej liczby naturalnej n ≥ 3 spełniona jest nierówność

2ⁿ > 2n [A]

Rozwiązanie:

Nierówność jest tu formą zdaniową T(n), n₀=3.

1. Dla n = 3 nierówność jest prawdziwa, ponieważ 2³ = 8 > 2*3 = 6. T(3) jest więc zdaniem prawdziwym.

2. Załóżmy, że nierówność jest prawdziwa dla liczby naturalnej n ≥ 3.

Mnożąc tę nierówność obustronnie przez 2 otrzymujemy 2*2ⁿ > 2*2n

czyli 2ⁿ⁺¹ > 2n + 2n

Ponieważ dla każdego n ≥ 3 mamy 2n > 2, więc 2n + 2n > 2n + 2 = 2(n + 1)

Stąd:

2ⁿ⁺¹ > 2(n + 1)

Nierówność ta oznacza prawdziwość zdania T(n+1). Wykazaliśmy zatem, że dla każdej liczby naturalnej n ≥ 3 prawdziwa jest implikacja T(n) ⇒ T(n+1), gdyż z prawdziwości jej poprzednika wynika prawdziwość następnika.

Ponieważ założenia 1 i 2 zasady indukcji matematycznej są dla nierówności [A] spełnione (n₀ = 3), więc ta nierówność jest prawdziwa dla każdego n ≥ 3.

QED

Przykład 2:

Udowodnić, że dla każdego naturalnego n

[A]

Rozwiązanie:

1. Sprawdzamy, że równość jest prawdziwa dla n = 1

2. Załóżmy, że równość jest prawdziwa dla liczby naturalnej n. Do obu stron tej równości dodajemy (n+1)², więc:

a następnie przekształcamy prawą stronę:

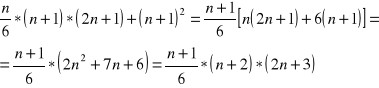
stąd:

Dla każdej liczby naturalnej n prawdziwa jest więc implikacja T(n) ⇒ T(n+1), gdzie T(n) oznacza równość [A]. Na mocy zasady indukcji matematycznej równość [A] jest więc prawdziwa dla każdej liczby naturalnej n.

QED

Przykład 3

Udowodnić, że dla każdego naturalnego n liczba
jest podzielna 6.

Rozwiązanie:

1. Dla n = 1 liczba
   
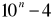
   jest podzielna przez 6, ponieważ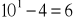
   jest podzielne przez 6.

2. Załóżmy następnie, że liczba
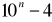
   jest podzielna przez 6.

Ale

a więc jest to też liczba podzielna przez 6.

Zgodnie z zasadą indukcji matematycznej świadczy to o tym, że liczba

jest podzielna przez 6 dla każdego n, będącego liczbą naturalną.

QED

Przykład 4

Udowodnić, że n różnych prostych leżących na płaszczyźnie i przechodzących przez dany punkt P dzieli tę płaszczyznę na 2n części.

Rozwiązanie:

1. Dla n = 1 twierdzenie jest prawdziwe, gdyż jedna prosta leżąca na płaszczyźnie i przechodząca przez punkt P dzieli tę płaszczyznę na 2 części, zaś 2 = 2*1

2. 
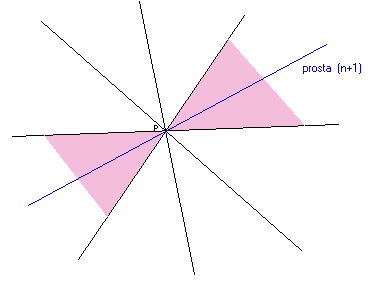
   Załóżmy, że przez punkt P przechodzi n różnych prostych leżących w jednej płaszczyźnie i że dzielą one tę płaszczyznę na 2n części. Poprowadźmy przez punkt P jeszcze jedną prostą leżącą w tej samej płaszczyźnie co poprzednie i różną od każdej z nich. Prosta o numerze (n+1) dzieli tylko dwie spośród 2n części płaszczyzny, przy czym każdą z nich na 2 części. Liczba części, na które podzielona jest płaszczyzna, wzrosła zatem o dwie (zobacz rysunek) i wynosi 2n + 2 = 2(n+1).

Wynika stąd, że twierdzenie jest prawdziwe dla liczby n + 1. Na podstawie zasady indukcji matematycznej twierdzenie jest prawdziwe dla każdej liczby naturalnej n.

QED

---