20.10.2009

Każde funkcje …………?????????????

Funkcję f określona następująco

ma wykres.

nie jest monotoniczna a mimo to jest wzajemnie jednoznaczna

Mówimy, że funkcja f odwzorowuje X na zbiór Y, jeżeli:

jeżeli nie zakłada się, że powyższy warunek zachodzi to mówimy, że f odwzorowuje X w Y.

Np. funkcja logarytmiczna

a>0 a≠1 x>0 odwzorowuje przedział
na przedział

Jeżeli funkcja f z X do Y jest jednocześnie iniekcją oraz surekcją to f nazywamy bijekcją X oraz Y.

Niech g będzie funkcją odwzorowującą X na Y, a f niech będzie funkcją odwzorowującą Y na Z, wtedy superpozycją, czyli złożenie funkcji f oraz g oznaczamy

odwzorowuje X w Z.

• 
  

WŁASNOŚCI SUPERPOZYCJI

• Łączność

• Nieprzemienność

W superpozycji
tzn. dla funkcji

funkcję g nazywamy funkcją wewnętrzną, a funkcję f funkcją zewnętrzną.

Przykład.

Funkcja złożona z funkcji
oraz
jest funkcja

Liczba

Funkcja f odwzorowuje wzajemnie jednoznacznie X na Y , wyznacza również x
X jako funkcję y
Y.

Otrzymaną w ten sposób funkcję oznaczamy przez f_-1 i nazywamy funkcją odwrotną do f to znaczy

Np. funkcją odwrotną do funkcji
jest funkcja
lub po zamianie nazw zmiennych
gdy

ZBIORY LICZB

• Naturalnych N={1,2…}

• Całkowitych Z={0,
  }

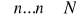
• Wymiernych W={
  }

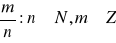
• Niewymiernych NW= np.
  

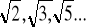
• Rzeczywistych R

Zachodzą inkluzje

FUNKCJE OGRANICZONE, MONOTONICZNE, WYPUKŁE, WKLĘSŁE

Funkcję

nazywany ograniczoną jeżeli

Funkcję

nazywany ograniczoną z góry (ograniczoną z dołu), jeżeli

Przykład

1. Funkcja signum

jest ograniczona, gdyż
dla każdego

2. Funkcja
dla
jest ograniczona z dołu, gdyż
dla

Niech
gdzie
mówimy, że

• f jest rosnąca na X jeżeli

• f jest malejąca na X jeżeli

• f jest nie malejąca na X jeżeli

• f jest nie rosnąca na X jeżeli

Funkcje te nazywamy monotonicznymi natomiast funkcję rosnące i funkcję malejące to tzw. funkcje ściśle monotonicznie.

Np. funkcja wykładnicza

y=f(x)=a^x gdy a>0 x
(-∞,+∞) jest rosnąca,

gdy a>1 oraz malejąca, gdy 0<a<1

Funkcja f odwzorowująca przedział
w zbiór
nazywamy wypukłą ( wklęsłą ) w
jeżeli

(
)

Np. funkcja wykładnicza f(x)=a^x jest wypukła

Np. funkcja logarytmiczna f(x)=log_ax jest wklęsła

FUNKCJE ELEMENTARNE

Oznaczmy

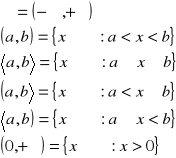
1. Funkcja stała

f(x)=C dla każdego x
X → dziedzina f, przy czym C jest liczbą rzeczywistą

2. Funkcja schodkowa

Niech
jeżeli funkcja f jest stała w każdym z przedziałów
to nazywamy ją funkcją schodkową ( nawiasy […] ozn. że funkcja
należy lub nie należy do przedziału)

Niech

3. Wielomiany

gdzie n jest liczbą całkowitą nieujemną

Jeżeli a₀≠0 to f jest wielomianem stopnia n.

Jeżeli
N to dziedziną wielomianu f jest
.

4. Funkcja wymierna

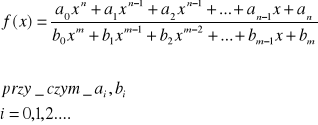
Funkcja wymierna f jest określona na
z pominięciem miejsc zerowych mianownika, przy założeniu, że licznik i mianownik nie posiadają wspólnych miejsc zerowych.

W szczególności funkcja f , gdzie

nazywamy funkcją homograficzną. Jest ona określona na zbiorze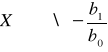

5. Funkcja potęgowa

Funkcja f określona równością

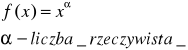
nazywamy funkcją potęgową.

Jeżeli

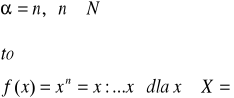
Jeżeli

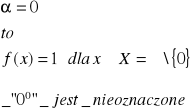
Jeżeli

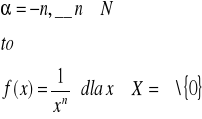
Jeżeli

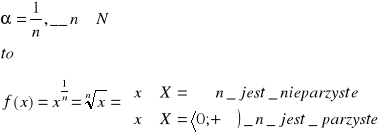
Jeżeli

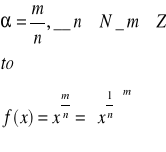
17

X

Y

Z

g na

f w

w

---