GRANICE FUNKCJI
Granica funkcji rzeczywistej jednej zmiennej.
Niech funkcja ![]()
![]()
będzie określona dla x takich, że 0<|x-x0|<a, a>0
Liczbę ![]()
nazywamy GRANICĄ FUNKCJI ![]()
w ![]()
jeżeli
![]()
Piszemy wtedy
![]()
lub ![]()
przy ![]()
Interpretacja geometryczna funkcji ![]()
![]()
Dla ![]()
WŁASNOŚCI FUNKCJI POSIADAJĄCYCH GRANICĘ:
Funkcja
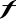
posiada w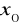
co najmniej jedną granicęNiech funkcja
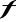
będzie określona dla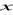
takich, że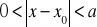
,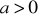
na to by funkcja ![]()
posiadała granicę ![]()
w ![]()
, potrzeba i wystarcza, by dla każdego ![]()
takiego, że ![]()
zbieżnego do ![]()
ciąg wartości funkcji ![]()
był zbieżny do ![]()
.
Jeżeli funkcja
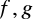
są określone w pewnym sąsiedztwie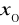
oraz posiada
granicę w ![]()
to, funkcja ![]()
![]()
posiada granicę w ![]()
oraz
![]()
![]()
Jeżeli ponadto ![]()
to i iloraz ![]()
posiada granicę w ![]()
oraz
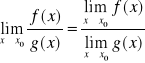
Jeżeli funkcja
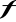
oraz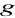
posiadają granicę w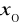
oraz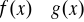
dla ![]()
,![]()
to ![]()
Twierdzenie o 3 funkcjach
Jeżeli funkcja ![]()
oraz ![]()
posiadają granicę ![]()
w ![]()
, oraz funkcja ![]()
jest określona i spełnia nierówność ![]()
w pewnym sąsiedztwie ![]()
, to ![]()
Niech funkcja ![]()
będzie określona dla ![]()
takich, że ![]()
![]()
. Mówimy, że funkcja ![]()
ma granicę prawostronną w ![]()
jeżeli istnieje liczba ![]()
spełniająca warunek
![]()
Niech funkcja ![]()
będzie określona dla ![]()
takich, że ![]()
![]()
. Mówimy, że funkcja ![]()
ma granicę lewostronną w ![]()
jeżeli istnieje liczba ![]()
spełniająca warunek
![]()
Piszemy wtedy
![]()
![]()
TWIERDZENIE 1
Niech funkcja ![]()
będzie określona dla ![]()
takich, że ![]()
![]()
.
Funkcja ![]()
ma granice ![]()
w punkcie ![]()
wtedy i tylko wtedy, gdy ![]()
posiada w ![]()
obie granice jednostronne ![]()
![]()
równe sobie ![]()
i równe ![]()
. ![]()
Skończoną granicę ![]()
funkcji ![]()
w ![]()
nazywamy granicą właściwą.
W przypadku funkcji nieograniczonej ![]()
w otoczeniu lub sąsiedztwie ![]()
, takich przy ![]()
mówimy o granicach niewłaściwych.
Niech funkcja ![]()
będzie określona dla ![]()
takich, że ![]()
![]()
.
Mówimy, że ![]()
posiada w ![]()
granicę
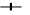
jeżeli: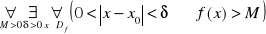
Piszemy wtedy ![]()
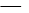
jeżeli: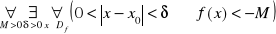
Piszemy wtedy ![]()
Podobnie jak dla granic skończonych można określić granice niewłaściwe jednostronne
Np. Funkcja ![]()
określona na przedziale ![]()
mamy,
![]()
Granice niewłaściwe przy ![]()
definiujemy następująco
![]()
![]()
TWIERDZENIE 2
Jeżeli
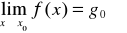
![]()
to ![]()
Jeżeli
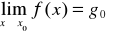
![]()
to ![]()
Jeżeli
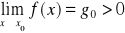
![]()
![]()
to ![]()
TWIERDZENIE O GRANICACH SUPERPOZYCJI FUNKCJI
Niech funkcja ![]()
będzie określona dla ![]()
takich, że ![]()
![]()
a funkcja ![]()
będzie określona dla ![]()
takich, że ![]()
![]()
Jeżeli ![]()
![]()
przy czym funkcja ![]()
nie przyjmuje wartości ![]()
dla ![]()
takich, że ![]()
to ![]()
TWIERDZENIE BOLZANO-COUCHY'EGO
Niech funkcja ![]()
będzie określona dla ![]()
takich, że ![]()
![]()
. ( lub ![]()
)
Na to, by funkcja ![]()
posiadała skończoną granicę przy ![]()
( lub ![]()
) potrzeba i wystarcza, by był spełniony warunek
![]()
(![]()
)
1
Wyszukiwarka
Podobne podstrony:
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
więcej podobnych podstron