DSC07334

86 Układy równań liniowych

Rozwiązanie

Dany układ zapisujemy w postaci

x + V    f 3

i    z + u    = 7 , stąd

tt+ V ; == 9 lOz    + v =15

1100 0'		z		3 *
0 110 0		V		5
0 0 110		z	=	n
0 0 0 1; 1		u		9
o o o o		V		. 15

:e

detali

Liczbę i obliczamy ze wzoru i =    S

det.4 =

110 0 0
Ó 1 10 0
0 0 110	=
0 0 0 1 1
10 0 0 0 1

1	1	0	0		0	1	0	0
0	1	1	0		0	II	1	0
0	0	1	1		0	a	1	1
0	0	0	1		10	0	0	1

	1	0	0
= 1+10	1	1	0
	0	1	1

3 1 0 0 0 5 1 I 0 0 7 0 110 9 0 0 1 1 15 0 0 0 1

	110 0		5 10 0
	0 110		7 1 10
= 3	0 0 11		9 0 1 1
	0 0 0 1		15 0 0 1

dct.4i -—

	1 1 0		7 10
3-5	0 1 1	+	9 11
	0 0 1		15 0 1

= -2+13 =

11.

• Przykład 4.4

Rozwiązać podane układy równań metodą macierzy odwrotnej:

a)

x + ly = 2 . 2x - y = 9*

b)

x — 2y + 3z = —7 3x + y + Az = 5 2x + 5y + z = 18

Rozwiązanie

Rozwiązanie X układu Cramera postaci y4X = B będziemy wyznaczać ze wzoru

X=A~^lB.

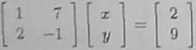
a) Zapisując układ równań w postaci macierzowej otrzymamy

Zatem

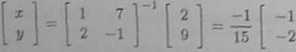
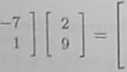
»- ^{13 1} c*yh * = -j. V =

b) Podobnie jak w poprzednim przykładzie mnożymy lewostronnie układ równań w postaci macierzowej przez macierz odwrotną do macierzy układu. Otrzymamy wtedy

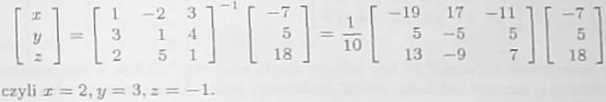
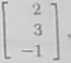
Rząd macierzy. Twierdzenie Kroneckera-Capellego

• Przykład 4.5

Znaleźć rzędy podanych macierzy wskazując niczerowe minory maksymalnych stopni:

				1	0	1	0	3'
'5	1	2 3"		0	0	0	0	0
1	4	-1 2	; b)	2	0	1	0	1
9	-2	5 4		0	0	0	0	0
				3	0	1	0	-1.

Rozwiązanie

Rzędem macierzy nazywamy największy stopień niczcrowcgo minora tej macierzy, czyli wyznacznika obliczonego z wybranych wierszy i kolumn tej macierzy, a) Dana macierz ma wymiar 3 x 4, a więc jej rząd może być równy 0,1.2 lub 3. Wartości 0 i 1 można od razu wykluczyć, gdyż łatwo wskazać niezerowy minor stopnia 2. np.

5    1

minor I ^    ,

1= 19 / 0 leżący w lewym górnym rogu macierzy. Należy teraz poszukać niezerowego minora stopnia 3. Obliczamy wszystkie możliwe minory stopnia 3. Mamy

5 12		5 13		5 2 3		1 2 3
i 4 -i 9-2 5	= 0,	1 4 2 9-2 4	= 0,	1 -1 2 9 5 4	= 0,	4-12 -2 5 4

Stąd wynika, że nie istnieje niezerowy minor stopnia 3, więc rząd danej macierzy jest równy 2.

b) Wszystkie minory danej macierzy zawierające parzyste wiersze lub parzyste kolumny są zerami. Minorem najwyższego stopnia nie zawierającym tych wierszy ani kolumn jest minor

= 0.

113 2 1 1 3 1-1

Stąd wynika, że rząd danej macierzy jest mniejszy od 3. Wśród minorów stopnia 2 istnieje

minor niezerowy, np.

1    1

2    1

= —1^0. Rząd danej macierzy jest więc równy 2.

• Przykład 4.6

Wykonując operacje elementarne na wierszach lub kolumnach podanych macierzy