DSC07336

90 Układy równań liniowych

Podobnie dla p = 2 mamy

	i p 1:		1 2 r
rz	3 0 2	= «	3 0 2
	,P “P l.		2 -2 u

tpj — Sto i

U13 — 2iO|

= rz

1 2 I 0 -6 -1 0 -6 -1

	1	2	l
u»a = rz	0	-6	-1

b) Łatwo sprawdzić, że wyznacznik danej macierzy jest równy 0 dla każdego p. To oznacza, że rząd tej macierzy nie jest nigdy równy 3. Zbadajmy teraz jeden z minorów stopnia 2, np. minor

P 1 2 2

= 2(p — 1).

Z postaci tego wyznacznika wynika, że dla p == 1 rząd danej macierzy jest równy 2. Dla p= l znajdujemy w macierzy inny niezerowy minor stopnia 2, np.

X 1		1 1
2 P-1		2 0

= -2^0.

Ostatecznie dla każdej wartości p 6 R rząd danej macierzy jest równy 2. c) Obliczmy jeden z minorów najwyższego stopnia np. minor

		ł-P	•-■21	1
		1	2-p			-p	'(4-p).
		1	2	1-p
Jeżeli ten	minor jest niezerowy,		tzn. jeżeli p 5Ś		0		zfi 4, to dana macierz
Przypadki p = 0 i p = 4 zbadamy			osobno	Dlap	s	= 0	mamy
	n-» 2 1	p'		1 2		0'	*12 = rz	1
rz	•— to j ta	* 0	= rz	l 2	l	0		0
	r l 2 1-	P P.		. 1 2	1	0.	U =0	1.

Natomiast dla p = 4 otrzymamy

	i-p 2 1 pi |	-3	2 14‘
rz	1 2-p 1 0| = rz	Ir-	-2 10
	1 2 i-ppJ	l	2 -3 4 J
		’ -3	2 14
= rz		1	-2 10
		4	0-4 0

103 —

U13 +

= 3.

• Przykład 4.9

W podanych układach równań liniowych określić (nie rozwiązując ich) liczby rozwiązań oraz parametrów:

	X	--	y + 2z + t = 1
	3x	+	y + z — t = 2
	. ^5x	—	y + 5z + t = 4
	X	—	3j/ + * = 0
	2x	+	V - z = 1
C)	5x	—	y — z = 2 ;
	X	—	10y + 4s = -1
	, ^x	-ł-	y + Iz = 1

{2x    +    2y    —    z    +    t    =    1

| *    —    V    -    z    +    3t    =    2    ;

3i    +    5y    -    4 2    -    t    =    O

{y + z + 3t = O 2x + V - z - 3£ = 2 x-2y + * + 2t«-l 2x + 3y + 2 + 3t =    1

Rozwiązanie

Zgodnie z twierdzeniem Kroneckera-Capellego układ równań liniowych z n niewiadomymi postaci AX = B może nie posiadać rozwiązań albo mieć dokładnie jedno rozwiązanie albo tez mieć nieskończenie wiele rozwiązań. Decydują o tym rzędy macierzy A układu oraz jego macierzy rozszerzonej [.4|fł| i wtedy odpowiednio mamy rz A ^ rz |/\|B) albo iz >4 = rz [j4|B| = n albo też rzA = rz [A\B] = r < n. W ostatnim przypadku zbiór rozwiązań zależy od n — r parametrów.

a) Rozważmy następujące przekształcenie macierzy rozszerzonej układu

’ 1 3	-l 1	2 1	1 —1	il	u>3 - 3u»i __ u>3 -		1 0	-1 4	2 —5	1 -4	1 -1
5	-1	5	1	4 J			0	4	-5	—4	-l

Z otrzymanej postaci wynika, że rz A — 2 — rz [/t|B| — r < n — 4. Oznacza to, że układ ma nieskończenie wiele rozwiązań zależących odn-r = 2 parametrów,

b) Zamieniamy dla wygody kolejność równań układu i przekształcamy jego macierz rozszerzoną do postaci

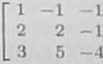
3	2'
1	1
-i	0

%bj - i*i

UP3 -

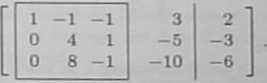
Stąd otrzymujemy, że rzA = 3 = rz [A\B\ = r. Jednocześnie n = 4, więc układ równań ma nieskończenie wiele rozwiązań, a liczba parametrów jest równa n — r = 1.

c) W tym przykładzie mamy n = 3. Stosując wskazane operacje elementarne kolejno otrzymamy

1	-3	1	°1		’ 1	-3	1	0'
2	1	-1	1	u>9 — 2»I	0	7	-3	1
5	-1	-1	2	w| — 5w| u'4 —	0	14	-6	2
1	-10	4	-1		0	— #	3	-1
L 1	1	2	1 .		. 0	4	1	1

*3= 2u»a «V4= -«2

Zatem rz>i = 3 = rz |/l|B| = n. Układ ma więc dokładnie jedno rozwiązanie.