50 51 (15)

50 . :    ... .. -Układy równań liniowych

dla p — 1 podobnie

	'2 p 1 p			2 1	1
rz	3 p P 1	= rz		3 1	1
	5p 1 f p 1 + p			5 2	2

Stąd wniosek, że podane wektory generują podprzestrzeń wymiaru 2 dla każdej wartości parametru p.

b) Tyra razem przeanalizujemy macierz współrzędnych danych wektorów w bazie u, i, w, x podprzestrzeni lin { u, v, w, z} C V tzn macierz

'314'

-p 1 4 3 1 p .~P 1 P .

Bez obliczeń łatwo zauważyć, że dla p = —3 pierwsze dwie kolumny są proporcjonalne i rząd macierzy jest równy 2 Podobnie dla p = 4 dwie ostatnie kolumny są proporcjonalne i rząd całej macierzy też jest równy 2. Dla p ^ — 3 i p ^ 4 wyznacznik stopnia 3 obliczony z pierwszych trzech wierszy jest jest różny od zera, więc rząd macierzy jest rówr.y 3 To oznacza, że dane wektory generują podprzestrzeń wymiaru 3 dla p ^ -3 i p ^ 4. Dla p =. — 3 lub p — 4 podprzestrzeń ta ma wymiar 2.

Zadania

C Zadanie 5.1

Znaleźć z definicji rzędy podanych macierzy wskazując niezerowc minory maksymalnych stopni:

		1	3	5“				' 2	3	-1		1'
b)		2	2	1	•		^c)	4	2	0		5
	.	1	0	3				0	4	-2		3
	' 1	0	1	0	I	o r		' 1	1	2	0	0"
	1	5	1	0	l	6 1		2	1	-1	0	0
<0	1	0	1	7	1	0 1	; 0	4	3	3	0	0
	1	8	1	0	1	9 1		0	0	0	7	5
	1	0	1	0	1	0 1		0	0	0	1	6

12    3

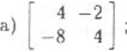
d)

2 1    -2

4 5    4    ¹

1 3    4

O Zadanie 5.2

Wykonując operacje elementarne na wierszach lub kolumnach podanych macierzy obliczyć ich rzędy:

	1-3 2 1 2 ‘		-2 1-3 1 -5'		'31621'
a)	2 1-13 1 4-5 356	; b)	45 15 30 -60 75 532-87	; <0	2    14 2 2 3    13 13 2 12 14

Piąty tydzień - zadania

<0

12    3    4

5 G 7 8 9 10 11 12    ¹

13 14 15 16

-4	l	l	1	1
:	-4	l	1	1
i	1	-4	1	1
i	1	l	-4	1
i	1	1	1	-4

O Zadanie 5.3

Sprowadzając podane macierze do postaci schodkowej wyznaczyć ich rzędy:

							r 4	1	2	5
	1	2	3	1	5"		0	1	3	4
*}	0	4	7	1	2	i b)	4	4	7	13
	1	2	3	4	6		1	1	-2	1
	-1	-2	-3	5	-3		8	5	5	14
							-4	-1	2	-1

c)    A = [a,;] jest macierzą wymiaru 5x7, gdzie a_t; = t+; dla 1 ^ i ^ 5, l ^ j ^

d)    B = [6,,] jest macierzą w^rymiaru 6x6, gdzie 6_|; = i²j dla 1 ^ i_tj ^ 6.

n

'11 1 o o o o

3 2 2 1 0 0 0 5 3 2 2 1 0 0 5 2 12 110 3 10 10 10 1 0 0 0 0 0 1

O Zadanie 5.4

Stosując algorytm Chió obliczyć rzędy podanych macierzy:

												' i	2	l	3	0	2
	2	3	1	2'		'3 -	1 4	4	7	1 '		2	1	-1	2	1	1
^a)	1	0	-1	1	; b)	2	1 0	-1	3	2	; c)	3	0	2	2 -1		4
	3	1	-i	4		8 -	1 8	7	17	1		6	3	2	7	0	7
	-2	2	0	3		7	1 4	2	13	5		1	-1	-2	-l	1	-1
												7	2	0	6	1	6

O Zadanie 5.5

Znaleźć rzędy podanych macierzy w zależności od parametru rzeczywistego p:

	lip'		'1 P 2		p - 1 p — 1 1 1
^a)	3 p 3 2p 2 2	; b)	1 -2 7 + p 1 2 + 2p -3 — p	; ^c)	1 p^2 - l 1 p - 1 1 p — 1 p — 1 1

d)

111 p

11 P V 1 P P V

; ^e)	p -p i -p -22-22	; n	p^2 4 4 4 4 p^2 2p 4 4 4
	3 p 3 p		p^2 2p 2|p| 4 4
	p 1 p 1		p^2 2p 2|p| 2' 4

O Zadanie 5.6

Zbadać liniową niezależność podanych wektorów we wskazanych przestrzeniach liniowych analizując rzędy macierzy ich współrzędnych w odpowiednich bazach: