62 63 (15)

62

r-    rarwlaate-

Układy równań liniowych

O Zadanie 6.2

Wskazać wszystkie możliwe zbiory niewiadomych, które mogą być parametrami określającymi rozwiązania podanych układów równań liniowych:

{z -    y +    z = -1    ( x 4- 2y 4-    3z    4- 4f = -1

2z + 2y - 2z =    3 ; b) ć -x + 8y 4- llz + 12* =    5 ;

3x +    y -    z =    2    ( 2x - y -    2    = —4

{r — 3y + 2 — 2s 4- i = —5 2x — 6y — 4.ę -H t = —10 2 2    4- < =    0

C Zadanie 6.3

Określić liczby rozwiązań podanych układów równań liniowych w zależności od parametru rzeczywistego p

1

-4 ;

-3

1

2

3    '

4

(    x    +    (p - 2)y    -    2pz    -    4

e)    C    px    +    (3 - p)y    +    42    =    1    .

I    0+p)x    +    V    +    2(2-p)z    =    7

a)

(P~ l)x 4- (2-p)y = p 1 - 3p)x 4- {p- 1 )y = -6

f px    4-    y    4-    2z    =    1

c)    < x    -ł    py    4-    2z    =    1    ;

[ x    4-    y    4-    2pz    =    1

(p-ł- l)x - y 4- pz b) ( (3 - p)x + 4y - p* pz + 3y

2r 4- py + pz 4- pi _d . 2r 4- 2y 4- pz 4- pi ' 2x + 2y + 2z 4- pi 2x 4- 2y 4- 2z 4- 21

O Zadanie* 6.4

Rozwiązać podane układy równań liniowych w zależności od wartości rzeczywistego parametru p :

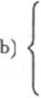
(    px    4-    3y    4-    24-    t    =    1

a)    <    2x    -    pz 4-    t    =    -2    ;

[    7x    4-    py    -    5z 4-    pi    =    -p

px 4    y    4-    P2    =    1

x 4-    y    4-    2    =    1

(2 - p)x 4- (2 - p)y    4-    2    =    1

px 4    y    4-    pz    =    p²

O Zadanie* 6.5

Rozwiązać podane układy równań liniowych dla n ^ 2 w zależności od parametru rzeczywistego p :

n 4- px₂ 4- ... 4- pr_n pz i 4* x₂ 4- .. 4* pz_n

pxi 4- px₂ 4-    4- x_n

= 1		' pxj	4- pz2 4- -	4- p*n = P
= 1 • I	b).	X\	4- px2 4- .	+ P*n = P
= 1		Xi	4- x2 4- •	4- pzn - p

a)

O Zadanie 6.6

W wytwórni montuje się wyroby A, B,C D, E z czterech typów detali a,b,c,d.

Szósty tydzień - odpowiedzi i wskazówki    63

Liczby dolali wchodzących w skład poszczególnych wyrobów podane są w tabeli

	A	B	C	D	E
a	1	2	0	4	1
b	2	1	^4	5	1
c	1	3	3	5	4
d	1	1	2	3	1

a)    Czy można obliczyć, ile ważą wyroby D i E, jeżeli wyroby A, B, C ważą odpowiednio 12, 20 i 19 dag. Podać znalezione wagi.

b)    Ile wazą detale a,b,c, jeżeli detal d waży 1 dag?

Odpowiedzi i wskazówki

G.l a), d) nieskończenie wiele rozwiązań, 1 parametr; b), c) brak rozwiązań; e) nieskończenie wiele rozwiązań, 2 parametry.

6.2    a) {y} {z}; b) wszystkie możliwe pary niewiadomych, tzr. {r,y], {z,*}, {*,<}>

{y.*}.    {*.*1; c) {z.y.z), {x_:y,.i}, {x,y,<}, {x,z,s}, {r.s.t}, {y,z,s}, {y,s,t}.

6.3    Układ nie ma rozwiązań, ma dokładnie jedno rozwiązanie, ma nieskończenie wiele rozwiązań odpowiednio a) dla p = —, dla p ^ — i p ^ 3, dla p = 3; b) nigdy, dla p £ 4 i p # 0. dla p = 4 lub p = 0, c) dla p = —2, dla p — 2 i p ^ 1, dla p = 1; d) dla p = 2, dla p 2, nigdy; e) dla p G R, nigdy, nigdy.

6.4    a) dla każdego p € R układ ma nieskończenie wiele rozwiązań: dla p = 3 rozwiązanie ma postać z = 3 — 3y — Az, t = —8 -ł- 6y -f 1 lz. gdzie y, z G i?, dla p = — ^ rozwiązanie

ma postać z = 0, z = — 2 + 2y, t = 3 - 5y, gdzie y € /i a dla p yi 3 i p ^ j rozwiązanie ma postać

r»l	' j ii	-1	l - pz	1	5 _ p2 -p — 5 1 + p		1 - px
^2 =	0 - P 1		-2 - 2x	= ■ . ■,-	p 2p -3		-2 - 2x
M	p -* p		-p - 1x	-2p^2 + p4 1S	p^2 Ib + p —3p .		-p-1x

b) dla p ^ — 1 i p 1 układ jest sprzeczny, dla p = — 1 ma dokładnie jedne rozwiązanie z = —1, y = 1. z = 1, dla p = 1 ma nieskończenie wiele rozwiązań postaci z = 1 — y - z, gdzie y, z £ R.

6.5 a) dla p = —-— układ jest sprzeczny, dla p ^ li p    —^:— ma dokładnie jedno roz-

1 — n    1 — n

wiązanie z\ = zj = ... = i_n = --, dla p = 1 ma nieskończenie wiele rozwiązań

1 + np - p

postaci xi -j-rj-ł- .. + Xn = 1; b) dla p ^ 0 i p 1 układ ma dokładnie jedno rozwiązanie Xj = ra = .    = iii-i = 0, x_n = 1, dla p = 0 ma nieskończenie wiele rozwiązań postaci

ii = Z2 = ... = Zn—i = 0, z_n € R, dla p == 1 ma nieskończenie wiele rozwiązań postaci *i + XJ + ... + Zn = !■

6.6    a) wyrób D waży 44 dag, zaś wagi wyrobu E na podstawie tych danych nie można uzyskać; b) detale a. 6, c ważą odpowiednio 4, 2 i 3 dag.