img038 3

84 U. Parametryczne testy istotności

nia (rozrzutu) wartości badanej cechy bywa szczególnie często w różnych badaniach naukowych wykorzystywana do oceny stopnia jednorodności czy też. powtarzalności wyników liczbowych uzyskiwanych w eksperymentach naukowych. W szczególności ocena dokładności przyrządu pomiarowego, za pomocą którego mierzy się wyniki eksperymentu, wymaga często sprawdzania hipotez o wariancji a¹ populacji. Wprawdzie odchylenie standardowe cr jest wygodniejszą w praktyce miarą rozproszenia niż wariancja, ale za to rozkład statystyki z próby' $, będącej estymatorem odchylenia standardowego, jest znacznie bardziej skomplikowany niż rozkład statystyki s², tzn. estymatora wariancji e². Ta ostatnia statystyka, odpowiednio przekształcona, ma bowiem znany i stablicowany rozkład y². Wygodnie jest zatem sprawdzić hipotezy nie o wartości odchylenia standardowego, lecz o wariancji.

Rozkład y²., z którym w tym paragraiie mamy do czynienia, został powszechnie stablicowany tylko dla liczby stopni swobody od 1 do 30. Ze względu na szybką zbieżność tego rozkładu do rozkładu normalnego, gdy liczba stopni swobody rośnie nieograniczenie, w praktycznych przypadkach w rozkładzie y^x dla liczby stopni swobody większej od 30 można już korzystać z rozkładu normalnego. Mianowicie, gdy liczba stopni swobody k w rozkładzie y² dąży do nieskończoności, dystrybuania zmiennej

►—- ■

losowej *J2%^a dąży' do dystrybuamy rozkładu normalnego N(\ 2k-\_y 1).

Dla liczby stopni swobody k większej od 30 zamiast z tablicy rozkładu x²

korzystamy więc z tablicy rozkładu A'{0. 1) dla zmiennej V2^² — -Jlk— I, Zc względu na to, że zwykle w praktyce jedynie większa wariancja od pewnej ustalonej jest niekorzystna, w poniższym teście istotności dla wariancji przyjmuje się zwykle obszar krytyczny prawostronny.

Model. Populacja generalna ma rozkład normalny N(m,o) o nieznanych parametrach m i g. Z populacji tej wylosowano niezależnie n elementów do próby, na podstawie której należy sprawdzić hipotezę //₀: rr²=<Xo» wobec hipotezy alternatywnej H_y: g²>gI> gdzie ^ jest hipotetyczną wartością wariancji o².

Test istotności dla lej hipotezy jest następujący. Z wyników n elementowej próby losowej obliczamy wartość s^z, a następnie wartość statystyki

•*    «-w.

(2.8)

°o

i" l

>'-5-

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ rozkład /} z a— 1 stopniami swobody, Dla ustalonego z góry poziomu istotności a j dla n— 1 stopni swobody odczytujemy z tablicy rozkładu taka wartość krytyczną aby Spełniona była równość P\y^z^-y‘} = x (O⁵- Nierów

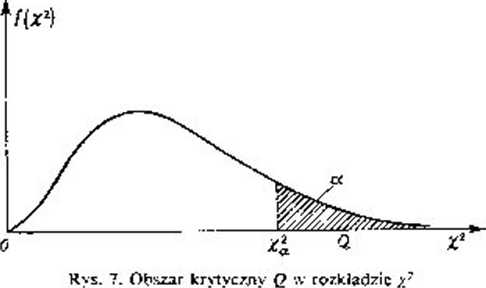
ność y~~2>y\ określa prawostronny obszar krytyczny, Izn. gdy z porównania wartości yy obliczonej z próby z wartością krytyczną y\ zajdzie nierówność X¹^xl - hipotezę W₀ odrzucamy na korzyść alternatywy //,. Natomiast gdy zajdzie nierówność x*</7* nie aria podstaw do odrzucenia hipotezy Ił#. że wartość wariancji o² populacji generalnej jest <7$.

Pr/.vki,a». Dokonano 12 pomiarów woltomierzem pewnego napięcia prądu i otrzymano z tej próby ś² = 0.9 V², Należy na poziomic istotności x = 0.05 sprawdzić hipotezę, że wariancja pomiarów napięcia tym woltomierzem wynosi 0.6

Ro-zwją^anie. W celu stwierdzenia, czy wariancja pomiarów nic jest Większa od wariancji hipotetycznej, stawiamy htpolozę fi_K.: c^l ■•0,6, wobec hipotezy alternatywnej //*: nⁱ>0,6.

Na podstawie wzoru (2-&) obliczamy z wyników próby wartość statysty k»

t>!w przyjętego poziomu istotności a =0,05 i dla w — ( = 11 stopni swobody odcżylujemy teraz Laką wartość krytyczną y\, aby P    ^: “t),05. Od-

czytanie to jest szczególnie łatwe, gdyż tablice rozkładu y} poda ją prawdo-