33 (457)

84 II. Parametryczne testy istotności

nia (fozrzutu) wartości badanej cechy bywa szczególnie często w różnych® badaniach naukowych wykorzystywana do oceny stopnia jednorodność^! czy też powtarzalności wyników liczbowych uzyskiwanych w eksperymen® tach naukowych. W szczególności ocena dokładności przyrządu pomiaró® wego, za pomocą którego mierzy się wyniki eksperymentu, wymaga częste® sprawdzania hipotez o wariancji a² populacji. Wprawdzie odchylenie stan-1 dardowe a jest wygodniejszą w praktyce miarą rozproszenia niż wariancja® ale za to rozkład statystyki z próby s, będącej estymatorem odchylenia® standardowego, jest znacznie bardziej skomplikowany niż rozkład statystyki® s², tzn. estymatora wariancji a². Ta ostatnia statystyka, odpowiednio® przekształcona, ma bowiem znany i stablicowany rozkład y². Wygodni® jest zatem sprawdzić¹ hipotezy nie o wartości odchylenia standardowego^! lecz o wariancji.

Rozkład y², z którym w tym paragrafie mamy do czynienia, zosta® powszechnie stablicowany tylko dla liczby stopni swobody od 1 do 30.® Ze względu na szybką zbieżność tego rozkładu do rozkładu normalneg^® gdy liczba stopni swobody rośnie nieograniczenie, w praktycznych przy]® padkach w rozkładzie y² dla liczby stopni swobody większej od 30 możni® już korzystać ż rozkładu normalnego. Mianowicie, gdy liczba stopni swo® body k w rozkładzie y² dąży do nieskończoności, dystrybuanta zmiennej 11 losowej V2y² dąży do dystrybuanty rozkładu) normalnego N(y]lk—\, l)a I Dla liczby stopni swobody k większej od 30 zamiast z tablicy rozkładu y²\ I korzystamy więc z tablicy rozkładu N(0,1) dla zmiennej v2x²—v2Ar—l! I Ze względu na to, że zwykle w praktyce jedynie większa wariancja od pewnej ustalonej jest niekorzystna, w poniższym teście istotności dla wariancji przyjmuje się zwykle obszar krytyczny prawostronny.

Model- Populacja generalna ma rozkład normalny N{m, a) o nieznanych parametrach m i a. Z populacji tej wylosowano niezależnie n elemenij tów do próby, na podstawie której należy sprawdzić hipotezę H₀: <r²=<r$M wobec hipotezy alternatywnej H_x: o²><jI, gdzie <7% jest hipotetyczną war]-' tpścią wariancji o²:

Test istotności dla tej hipotezy jest następujący. Z wyników n element® wej próby losowej obliczamy wartość s², a następnie wartość statysty la

1 )s

^; ₂ ns² (n-

. ⁼rz2 " °0

(2-8)

7=4 i

<?0 i=l

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ rozkład x^{2 v}- n — \ stopniami swobody. Dla ustalonego z góry poziomu istotności cc i dla n— 1 stopni swobody odczytujemy z tablicy rozkładu x² taką wartość krytyczną.^, aby spełniona była równość P{x²**xl}--<x (rys. 7). Nierów

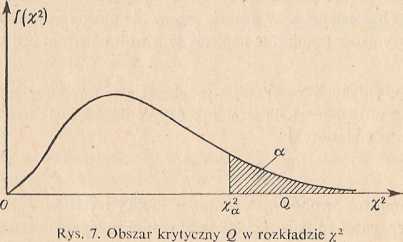
ność x^xi określa prawostronny obszar krytyczny, tzn. gdy z porównania wartości y², obliczonej z próby z wartością krytyczną *²zajdzie nierówność X²^xl-hipotezę H₀ odrzucamy na korzyść alternatywy H_x. Natomiast gdy zajdzie, nierówność x² <xl> nie ma podstaw do odrzucenia hipotezy //₀, że wartość wariancji a² populacji generalnej jest o\.

Przykład. Dokonano 12 pomiarów woltomierzem pewnego napięcia prądu i otrzymano z tej próby s²=0,9 V². Należy na poziomie istotności a = 0,05 sprawdzić hipotezę, że wariancja pomiarów napięcia tym wolto-^-mierzem wynosi 0,6 V²

Rozwiązanie. W celu stwierdzenia, czy wariancja pomiarów nie jest większa od wariancji hipotetycznej, stawiamy hipotezę H₀: a²=0,6, wobec hipotezy alternatywnej H_x: a² >0,6.

Na podstawie wzoru (2.8) obliczamy z wyników próby wartość statystyki

Dla przyjętego poziomu istotności a = 0,05 i dla n— 1 = 11 stopni swobody odczytujemy teraz taką wartość krytyczną xl-< aby P(/²^^²} = 0.05. Odczytanie to jest szczególnie łatwe, gdyż tablice rozkładu x² podają prawdo-