Matematyka 2 03

302 IV. Równania różniczkowe zwyczajne

7. PEWNE WIADOMOŚCI O UKŁADACH RÓWNAŃ RÓŻNICZKOWYCH.

PODSTAWOWE OKREŚLENIA. Niech będzie dany układ równań różniczkowych postaci

dx

(7.1)

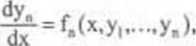
gdzie y_k, k = l,...,n, oznaczają niewiadome funkcje zmiennej x, a

f_k, k = l.....n, są funkcjami ciągłymi na pewnym obszarze DcR"*¹.

Jak widać, jest to układ równań różniczkowych rzędu pierwszego, rozwiązanych względem pochodnych niewiadomych funkcji. Układ tej postaci nazywamy układem normalnym.

Rozwiązaniem szczególnym układu (7.1) na przedziale I nazywamy każdy układ n funkcji

(7.2)    y, = y,(x).....y» = y_B(x), x€i,

xel, przy czym (x.y,(x),....y_n(x))eD dla dowolnego xel. Inaczej mówiąc, równania (7.1) dla funkcji (7.2) stają się tożsamościami na przedziale I.

Lawo na przykład sprawdzić,*żc para funkcji u = x+e²\ v = e'²\ xeR, jest rozwiązaniem szczególnym układu równań

du v + 2

dx v ¹ dv 2

dx x-u

Układ ten rozważamy przy założeniu, że u*x i v*0. Podane

funkcje u(x) i v(x) warunki te spełniają. Po obliczeniu pochodnych

du dy. | _wslawj_enj_u d₀ danego układu otrzymujemy równości dx^ł dx

"²* + 2

„ -2x

l + 2e²* =—

które są tożsamośćiami. Zatem para funkcji

u= x + c²\ v = e"²*. x eR, jest rozwiązaniem danego układu równań.

Rozwiązaniem ogólnym układu (7.1) nazywamy układ n funkeji postaci

(7.3)    y, = y,(x,c,.....C„).....y_n » y_n(x.C,.....C_D)

(C,.....C„ oznaczają tu dowolne stałe) mający tę własność, że dla dowolnego dopuszczalnego układu stałych    funkcje (7.3) stanowią

pewne rozwiązanie układu (7.1).

Zagadnienie Cauchy’cgo dla układu równań różniczkowych (7 I) jest to zadanie polegające na znalezieniu takiego rozwiązania

y_t = y₍(x).....y„=y„(>t)

tego układu, które spełnia warunki

yi<x₀) = y?.....y„(Xo) = y!

dla danych liczb x_0tyf.....y°„.

W dalszych rozważaniach ograniczymy się do układów w postaci normalnej. Warto jednak zauważyć, że ograniczenie to nie jest bardzo istotne Wiele układów równań zapisanych w innej postaci mpżna sprowadzić do układu normalnego. Na przykład łatwo wykazać, żc każdy układ równań rozwiązanych ze względu na najwyższe pochodne niewiadomych funkcji (tzw. układ standardowy) można sprowadzić do układu normalnego poprzez wprowadzenie pomocniczych niewiadomych. Ilustruje to następujący przykład.