CCF20090701021

40 E. Cassirer - O teorii względności Einsteina

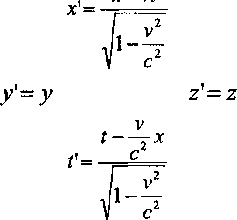
Zgodnie z tymi równaniami widzimy, że prawo rozchodzenia się światła w próżni jest w równym stopniu spełnione dla każdego uzasadnionego systemu K i K’; z drugiej zaś strony, że podstawowe elektrodynamiczne równania Maxwella nie zmieniają swej formy, gdy zamiast formuły transformacji Galileusza zastosuje się do nich transformację Lorentza. Jest to zatem uniwersalna zasada względności obejmująca całość zjawisk fizycznych; prawa, zgodnie z którymi zmienia się stan układu fizycznego, są niezależne od tego czy odnoszą się do jednego, czy do drugiego z dwu układów współrzędnych poruszających się względem siebie ruchem jednostajnym (por. 16, s. 29). Zasada względności mechaniki klasycznej nie tyle przeczy tej generalnej zasadzie, co raczej zawiera się w niej jako szczególny przypadek; równania transformacji Galileusza wynikają wprost z równań transformacji Lorentza, jeśli tylko dotyczą takich prędkości v, które są bardzo małe w porównaniu z prędkością światła, tak że wartość

V V

^ — może praktycznie zostać pominięta w obliczeniach. Wynika to z tego,

C G

że zasada względności elektrodynamiki, przeniesiona do mechaniki nie przeczy żadnym wynikom empirycznym, podczas gdy przeniesienie zasady względności mechaniki do elektrodynamiki okazuje się, jak uczy porażka teorii Hertza, niemożliwe. Gdy przyjrzeć się temu bliżej, procesy elektrodynamiczne nie mogą w szczególnej teorii względności w żadnym wypadku służyć jako klucz dla mechanicznych, ale została w nich ustanowiona prawdziwie uniwersalna zasada, „heurystyczna maksyma” badania w ogóle, która chce zawierać kryterium zasadności i dopuszczalności dla wszystkich szczególnych dziedzin i teorii fizycznych. Początkowa sprzeczność, widoczna pomiędzy zasadami mechaniki i elektrodynamiki, okazała się zatem drogą do dużo doskonalszej i głębszej jedności pomiędzy nimi niż ta, która miała miejsce wcześniej. I sukces ten nie został osiągnięty poprzez mnożenie eksperymentów, poprzez na nowo wszczynane badania, lecz polegał na krytycznym przekształceniu systemu podstawowych pojęć fizyki.

Od strony czysto epistemologicznej jawi się zatem jeszcze wyraźniej, że temu intelektualnemu procesowi, któremu zawdzięcza swe powstanie teoria względności, sprzeciwia się ten specyficzny „przewrót kopemikań-ski”, ta przemiana w pojęciowych podstawach przyrodoznawstwa, którą przeprowadziliśmy wcześniej na przykładzie mechaniki klasycznej i wcześniejszej fizyki. Istotna część tego osiągnięcia wydaje się opierać na tym, że przesunęła ona wcześniejsze logiczne stałe fizycznego poznania, że postawiła je na innym miejscu niż przedtem. Dla mechaniki klasycznej stały i nieruchomy punkt był założeniem tożsamości przestrzennych i czasowych wartości uzyskanych poprzez pomiar w różnych systemach. Ta tożsamość miała być niekwestionowanym i pewnym fundamentem pojęcia obiektywności w ogóle: jako ta, która pierwsza właściwie konstytuuje przedmiot „przyrody” jako przedmiot geometryczno-mechaniczny i odróżnia go od zmiennych i relatywnych danych wrażeń zmysłowych. Tó pev axrjpot, kołG’ auto son, to 5s yA,uku Kai ożi&ę ala0r|TÓv rcpóę aXXo Kai sv ażAoię - brzmi twierdzenie, które już Demokryt wprowadził jako podstawę atomizmu, a które w czasach nowożytnych zostało użyte przez Galileusza do poparcia podstawowego rozróżnienia pomiędzy jako-ściami „pierwotnymi” i „wtórnymi”, a zatem całego „mechanicznego” obrazu świata. Mimo że ustanowiona tu zasada udowodniła swoją przydatność i była często potwierdzana w strukturze fizyki matematycznej, nowożytny rozwój fizyki coraz wyraźniej pokazał, że była ona pojmowana zbyt wąsko w filozoficznym i metodologicznym sensie. Prawdziwym celem fizyki nie jest mechanizm, lecz jedność, jak swego czasu Henri Poincare sformułował przewodnią maksymę nowożytnej fizyki. Jednak w stosunku do tej jedności fizycy nie potrzebują pytać czy ona zachodzi, lecz jak ona zachodzi, to znaczy, jakie jest minimum założeń, które są konieczne i wystarczające dla dostarczenia jednoznacznego przedstawienia całości doświadczenia i jego systematycznego powiązania (72, s. 172 i nast.). Aby utrzymać tę jedność, która wydaje się być zagrożona przez konflikt zasady stałości prędkości światła i zasady względności mechaniki, oraz by uzasadnić ją głębiej i mocniej, teoria względności wyrzeka się stałości odległości przestrzennych i czasowych w różnych układach. Rezygnuje ona z założenia, że interwał czasowy pomiędzy dwoma zdarzeniami jest wielkością ustaloną raz na zawsze, niezależnie od stanu