Xerox Phaser200MFP 081126112124

44 Janusz Buga, Helena Kassyk-Rokicka

nostek zbiorowości. Ma ono zastosowanie szczególnie w tej sytuacji, gdy nie można obliczyć średniej arytmetycznej, a poziom przeciętny jest scharakteryzowany za pomocą kwarty Ii.

Podstawową miarą zmienności cechy w zbiorowości jest wariancja oraz pierwiastek kwadratowy z wariancji zwany odchyleniem standardowym.

tości cechy od średniej arytmetycznej tej cechy w danej populacji¹³. Dla szeregu prostego wariancję określa wzór:

Wariancja jest to średnia kwadratów odchyleń poszczególnych war-

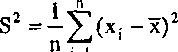
(2.14)

1 = 4

natomiast dla szeregu rozdzielczego:

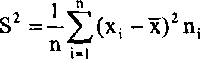
(2.15)

We wzorze (2.15) w miejsce wag n* można wstawić wskaźniki struktury w,-. Jeżeli w szeregu rozdzielczym cecha jest scharakteryzowana w przedziałach klasowych, wtedy jako wartość X; bierzemy wartość środka przedziału klasowego X;. W zastosowaniach praktycznych istotne jest, by zróżnicowanie wartości cechy można było wyrazić w miarach zgodnych z mianem badanej cechy. Aby właśnie tak się stało należy obliczyć pierwiastek kwadratowy z wariancji, który nazywamy odchyleniem standardowym. Tę miarę, oznaczaną symbolem S, wykorzystuje się w praktyce powszechnie.

Przykład 2.14

Przeanalizujemy kwestię zmienności cechy rozpatrując wydajność pracy trzech pracowników, wytwarzających te same detale w różnych dniach tygodnia.

¹³ Por. S. Ostasiewicz i in., op.cit., s. 61.

Tabl. 13. Dzienna wydajność (w sztukach detali)

Dzień	Pracownik I	Pracownik II	Pracownik III
1	6	7	10
2	12	11	10
3	8	12	10
4	10	8	10
5	12	10	8
Razem	48	48	48

Okazuje się, że średnia wydajność pracy każdego z trzech pracowni

ków w ciągu tygodnia jest identyczna i wynosi: x = — = 9,6 sztuk.

Mimo iż łączne wydajności pracowników są sobie równe, to łatwo zauważyć, że dzienne wydajności poszczególnych pracowników różnią się między sobą. Najbardziej rytmicznie pracował pracownik III, gdyż dopiero w ostatnim dniu tygodnia efekt jego dziennej wydajności obniżył się w stosunku do wydajności w poprzednich dniach. Z danych tablicy 13 wynika, że średnia arytmetyczna nie może być wykorzystana do oceny zróżnicowania wartości cechy w populacji, gdyż wartości Arednie mogą być identyczne, a mimo to badane populacje są zróżnicowane pod względem wartości danej cechy.

Wykorzystajmy dane tablicy 13 do obliczenia wariancji i odchylenia Bttmdardowego dla wydajności poszczególnych pracowników w ciągu pięciu dni roboczych.

Pracownik I

Wydajność (w sztukach)	(Xj - x)	(x,-x)^2
6	-3,6	12,96
12	2,4	5,76
8	-1,6	2,56
10	0,4	0,16
12	2,4	5,76
I Kazein	X	27,20