Xerox Phaser200MFP 081126111806

30 Janusz Buga, Helena Kassyk-Rokicka

Średnia arytmetyczna ma ważne własności, z których wymienimy następujące:

a)    suma wartości cechy równa się iloczynowi średniej arytmetycznej przez liczebność zbiorowości;

b)    średnia arytmetyczna spełnia warunek:

X_min<X<X_max,

tzn., że x jest większa od najmniejszej wartości cechy w zbiorowości i jednocześnie jest mniejsza od największej wartości cechy w tej zbiorowości;

c)    suma odchyleń (różnic) poszczególnych wartości cechy od średniej arytmetycznej równa się zeru:

n

n

d)    średnią arytmetyczną wyznacza się z szeregów z zamkniętymi przedziałami klasowymi. Doświadczenia praktyczne wskazują, że można domknąć przedział (przedziały) otwarty, jeżeli liczebność tego przedziału (przedziałów) jest niewielka - praktycznie nie przekracza 5% liczebności całej zbiorowości;

e)    średnia arytmetyczna nie jest właściwą miarą dla zbiorowości niejednorodnych, czyli takich, w których występują istotne różnice między poszczególnymi wartościami badanej cechy. Obliczanie np. średniej arytmetycznej dla populacji pracowników zatrudnionych w pewnej firmie, w której dziesięciu pracowników zarabia miesięcznie po ok. 3500 zł, natomiast czterech zarabia po ok. 20000 zł traci sens poznawczy. Przy powyższych danych średnia płaca jest równa ponad 8270 zł, co nie oddaje rzeczywistego stanu rzeczy;

f)    średnia arytmetyczna jest wrażliwa na skrajne wartości cechy. Należy właściwie ocenić tego rodzaju obserwacje: czy np. nie zostały one przypadkowo włączone do zbiorowości. W pewnych sytuacjach można takich wartości nie brać pod uwagę.

2.3.2. Średnia harmoniczna

Jest to ten rodzaj średniej, która w wykładach i podręcznikach jest pomijana, gdyż ma ona zastosowanie nie do szeregów rozdzielczych, z którymi się zapoznaliśmy, lecz do szeregów, które niektórzy autorzy określają jako guasi-rozdzielcze. Są to szeregi, w których obok wariantów badanej cechy nie występują liczebności (częstości), lecz pewne wielkości, tworzące logiczny związek z tymi wariantami. Na przykład, aby obliczyć przeciętną cenę targowiskową marchwi dysponujemy informacjami o cenie kg marchwi w kilku punktach sprzedaży i wysokości ich utargu. Zestawienie niezbędnych danych liczbowych może mieć następującą postać:

Punkty sprzedaży	A	B	C	D
Cena zł/kg	0,60	0,75	0,65	0,85
Utarg w zł	29,00	35,00	36,00	19,00

Na podstawie tego rodzaju danych wyznaczanie wartości średniej arytmetycznej nie ma sensu. Powiada się, że średnią harmoniczną stosujemy wówczas, gdy wartości cechy podane są w przeliczeniu na stałą jednostkę innej zmiennej, czyli w postaci tzw. wskaźników natężenia. Są to przykładowo takie cechy, jak: prędkość pojazdu mechanicznego na godzinę, wydajności pracy w sztukach na godzinę, liczba łóżek w szpitalach na 10000 mieszkańców itp. I tak, dla szeregu szczegółowego (warianty cechy występują w postaci uporządkowanego ciągu liczb) mamy:

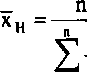
(2.4)

Ola szeregu rozdzielczego (dla każdej wartości cechy podana jest jej liczebność):

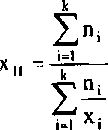
(2.5)