Xerox Phaser200MFP 081126111954

38 Janusz Buga, Helena Kassyk-Rokicka

ⁿq,=

3(n + l)

Przechodzimy do przykładu. I tak:

^[Qi

N„ =Iil=2;

7 + 1

^N*’= 2

= 4;

Odnajdujemy w uporządkowanym szeregu empirycznym miejsca zajmowane przez poszczególne kwarty le, zaznaczając wartości cechy znajdujące się na tych miejscach w badanej populacji pracowników:

2,5,15,17,18,20,21,

a zatem Q_t - 5; Q₂ = 17; Q3 = 20.

Inteipretacja wyników jest następująca: kwartyl pierwszy - 25% badanych pracowników opuściło mniej niż 5 dni w półroczu, a 75% pracowników opuściło więcej niż 5 dni; kwartyl drugi - 50% pracowników populacji badanej opuściło nie więcej niż 17 dni, a 50% pracowników opuściło więcej niż 17 dni; kwartyl trzeci - 75% pracowników opuściło nie więcej niż 20 dni, a 25% - więcej niż 20 dni.

Uwaga: jeżeli liczba elementów populacji jest liczbą parzystą, wówczas:

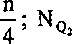
n + 1 3n

-; N_n = —.

2 ^Qi 4

Może się zdarzyć, że pozycja kwartyla nie jest liczbą całkowitą. Wówczas bierzemy pod uwagę średnią arytmetyczną z wartości cech znajdujących się na miejscu poprzedzającym i następującym po numerze pozycji właściwej dla danego kwartyla.

Przykład 2.10

Załóżmy, że uporządkowana wg rosnących wartości cechy zbiorowość jest następująca;

2,4, 5, 6, 8, 9, 10,11,13, 15.

Należy obliczyć wartości kwartyli: pierwszego, drugiego, trzeciego. Rozwiązanie

Pozycje odpowiednich kwartyli to:

*_T 10 ^ 10 + 1 _XT 3-10 _

N_Q| - ^ -2,5; Nq₂ - ^ ⁿq₃ ~ ą -7£.

W celu obliczenia kwartyla pierwszego wyznaczamy średnią arytmetyczną z wartości cech znajdujących się na pozycji drugiej i trzeciej, czyli:

4 + 5

Q‘=—-4+

Analogicznie postępujemy w przypadku kwartyla drugiego, czyli

mediany:

8 + 9

Q₂ (Me) = ~~~ - 8,5.

Natomiast wartość kwartyla trzeciego jest równa:

^ 10 + 11 Q₃—— = 10,5.

Interpretację otrzymanych wyników pozostawiamy Czytelnikom.

W przypadku, gdy przedmiotem analizy jest szereg rozdzielczy z przedziałami klasowymi, postępowanie przypomina procedurę, jaką zastosowaliśmy przy znajdowaniu wartości modalnej. Wzór pozwalający wyznaczyć dowolny z trzech kwartyli ma następującą postać:

ⁿq, - Z "i

(2.9)

•h,

Qi=*» +-—

ⁿQi

i)_t - kwartyl o numerze i (i = 1,2, 3),