Xerox Phaser200MFP 081126111700

26 Janusz Buga, Helena Kassyk-Rokicka

czyli:

26 Janusz Buga, Helena Kassyk-Rokicka

_ X, +X, +X, + ... + X_f

X -

n

(2.1)

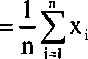
W tym przypadku przyjęliśmy, że badana zbiorowość składa się z n-elementów o wartościach cechy xj, x₂,..., x_n.

Przykład 2.1

W klasach drugich pewnego liceum ogólnokształcącego zbadano na koniec pierwszego półrocza poziom ocen z języka polskiego. W klasie Ha wybrani losowo uczniowie otrzymali następujące oceny: 3. 4, 5, 2, 3, 2, 6, 4, 3, 5. W klasie Ilb identyczna liczba uczniów uzyskała oceny; 2, 3, 3, 5, 4, 3, 6, 6, 4, 2. Jaka była średnia ocen z języka polskiego w każdej z dwóch analizowanych klas.

Rozwiązanie

x„ -

Xu =

3+4+5+2+3+2+6+4+3+5

_ .

2+3+3+S+4+3+6+6+4+2

—

37

⁼To ^=3,7

=— = 3,8 10

W klasie Ila średnia ocen z języka polskiego wyniosła na koniec pierwszego półrocza 3,7, natomiast w klasie Ilb 3,8. Można powiedzieć, że oceny uzyskiwane przez uczniów z języka polskiego były podobne, z tym, że w Ilb były one, przeciętnie biorąc, nieco lepsze (wyższe).

Przypuśćmy, że w toku tego samego badania zebrano informacje o liczbie uczniów, którzy otrzymali konkretną ocenę. W takim przypadku powiemy, że każda wartość cechy (tzn. ocena) ma przyporządkowaną jej liczbę uczniów. Jeżeli badana cecha posiada k wartości (wariantów), tzn. xj, x₂, ..., x_k, a liczba elementów, które przyjmują kolejne wartości cechy jest odpowiednio ni, n₂,..., n_k, przy czym:

k

Xⁿi^=I1’

i=i

to wówczas średnia arytmetyczna wyraża się następującym wzorem:

-_^x\ⁿ\ + x₂n₂+... + x_kn_k n, + n₂ +.„ + n_k

który w postaci skróconej, używając symbolu sigmy można zapisać

k    k

X =

(2.2)

i=l

Taką postać średniej arytmetycznej nazywamy średnią arytmetyczną ważoną, przy czym wagami są tutaj liczebności ri[ odpowiadające poszczególnym wartościom cechy.

Przykład 2.2

Pozostajemy przy treści zadania 2.1 z tym, że wartościom cechy przyporządkowano liczebności. Dla ułatwienia zestawimy odpowiednie ilane w tablicy 8.

Tabl. 8. Rozkład badanej cechy x wśród uczniów klas Ila i Ilb liceum ogólnokształcącego w I półroczu

Rozkład ocen z języka polskiego X;	Liczba uczniów klasy Ila n;	Liczba uczniów klasy Ilb n;	n;-Xi dla klasy Ila	nrXi dla klasy Ilb
(2) niedostateczna	5	4	10	8
(.1) dostateczna	10	11	30	33
(4) dobra	5	6	20	24
(5) h. dobra	10	7	50	35
ló) wyróżniająca	8	6	48	36
i iHÓlem	38	34	158	136