Xerox Phaser200MFP 081126112310

50 Janusz Buga, Helena Kassyk-Rokicka

leniem standardowym, wówczas można wyznaczyć tzw. typowy obszar zmienności badanej cechy. Definiuje go następująca relacja: x-S<x_lyp <x + S

W typowym obszarze zmienności mieszczą się wartości cechy około 2/3 wszystkich jednostek badanej zbiorowości statystycznej.

2.4.1. Asymetria i sposób jej pomiaru

Można spotkać takie sytuacje, gdy oszacowanie średniej wartości cechy oraz jej rozproszenia nie wskazuje, że istnieją różnice między badanymi populacjami. Zdarza się bowiem, że średnia arytmetyczna i wariancja przyjmują odpowiednio jednakowe wartości, jednak nie musi to wcale oznaczać, że rozważane populacje są identyczne pod względem struktury jednostek badanych cech. Empiryczny ich rozkład może wskazywać, że mamy do czynienia z różnymi jego postaciami w populacji. Wyróżniamy w szczególności rozkłady asymetryczne, w tym rozkłady z asymetrią prawostronną i lewostronną. Do oceny kierunku i siły asymetrii używa się dość często współczynnika asymetrii, czyli skośno-ści. Punktem wyjścia do jego konstrukcji jest porównanie dwóch rodzajów średnich: dominanty (Do) oraz średniej arytmetycznej (x). Różnica x - Do wskazuje na kierunek asymetrii. I tak, jeżeli x > Do, wtedy mamy do czynienia z asymetrią prawostronną, jeżeli x < Do, wówczas występuje asymetria lewostronna. Aby uniknąć kłopotów przy porównywaniu siły asymetrii, posługujemy się miarą względną, to znaczy różnicę x - Do dzielimy przez odchylenie standardowe. W konsekwencji tzw. współczynnik asymetrii (lub skośności) A_s przyjmie postać:

A =

(2.18)

x-Do

s

Współczynnik A_s najczęściej przyjmuje wartości z przedziału +1 i -1. Może się jednak zdarzyć, że przekroczy on wartość 111, co będzie wskazywać na bardzo silną asymetrię. Jeżeli A_s - 0, to oznacza, że średnia arytmetyczna jest równa dominancie, a tym samym wskazuje na symetryczny rozkład cechy.

Należy podkreślić, że współczynnik As jest jedynie przybliżoną miarą skośności. Zależności bardziej złożone pomijamy, gdyż wykraczają one poza treść niniejszego podręcznika.

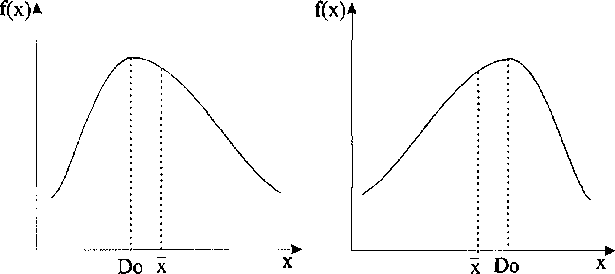
Rys. la    Rys. Ib

Przykład 2.16

Zbadano liczbę uczniów w szkołach w miastach i na wsi, w których Płl określone liczby nauczycieli. Chodzi o to, jaka liczba uczniów szkół tłezy się w szkołach zatrudniających określoną liczbę nauczycieli, odrębnie w miastach i na wsi. Okazało się, że na szkoły o liczbie nauczycieli od 1 do 5 przypada zaledwie około 10 tys. uczniów w miastach i jhiHłitf 56 tys. uczniów na wsi. W szkołach miejskich o liczbie nauczycieli od 36 do 40 uczy się ponad 2 min uczniów, podczas gdy na wsi jedynie około 61 tys. uczniów. Mamy więc do czynienia z asymetrycznym rozkładem cechy, Z braku miejsca pominiemy tutaj analizę danych Bjfóitogó(owych, podając od razu wartości potrzebne do obliczeń mierników. ! tak, w miastach na jednego ucznia przypadało średnio 34 na-tleli, a we wsiach 16 nauczycieli. Wartość dominanty dla miast bylit równa 40, a dla wsi 12. Odchylenie standardowe dla miast wynio-nln 1,2, natomiast dla wsi 8,1. Na podstawie powyższych danych mo-^r *Hny obliczyć współczynniki asymetrii dla miast i dla wsi.