Xerox Phaser200MFP 081126111834

32 Janusz Buga, Helena Kassyk-Rokicka

Przykład 2.4

Zaobserwowano, że w ciągu ośmiu godzin pracownik A potrzebował na wykonanie detalu 6 minut, pracownik B - 8 minut, natomiast pracownik C - 10 minut. Ile czasu, przeciętnie biorąc, potrzebują ci pracownicy na wykonanie jednego detalu.

Rozwiązanie

Stosując wzór (2.4) otrzymujemy

3 n n •

X_H = 1 ~f = ⁷-⁷ “““•

— H---1--

6 8 10

Gdybyśmy zastosowali średnią arytmetyczną, wówczas wynik byłby;

a więc różny od wyniku, który otrzymaliśmy wyżej.

Przykład 2.5

Samochód ciężarowy rozwożący towary z hurtowni do sklepów przebył trasę 10 km z prędkością 40 km/godz., natomiast wracając do hurtowni jechał z prędkością 60 km/godz. Jaka była średnia prędkość samochodu?

Rozwiązanie

Zauważymy, że w przykładzie n = 2, gdyż są dwie obserwacje -dwie trasy po 10 km. Tak więc;

2 2 240 ,_{D1 ; 4}

x_H = —-j- = —= —= 48 ^krn/8^odz-

40 ⁺ 60 120

Przykład 2.6

W hurtowni wartość trzech artykułów A, B, C o określonej cenie jednostkowej kształtowała się następująco:

Artykuł	Cena jednostkowa (W Zł) Xi	Wartości artykułów (w zł) Xin_}
A	5	30
B	10	50
C	20	120

Jaka była przeciętna cena jednostkowa trzech artykułów?

Średnia cena trzech analizowanych artykułów wyniosła 11,8 zł. 2.3.3. Średnia geometryczna

Średnią geometryczną n liczb jest pierwiastek stopnia n z iloczynu łych liczb. Wykorzystywana jest ona często do badania takich zbiorowości, w których wartości jednostek są przedstawiane w liczbach względnych. Należy podkreślić, że średnia geometryczna jest mniej wrażliwa na wartości skrajne - ekstremalne, aniżeli średnia arytmetycz-mi.

Średnią geometryczną wyznaczamy wg wzoru:

x_g = ^x, *x₂-...-x_n (2.6)

lub wykorzystując skrócony symbol iloczynu II

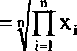
(2.7)

Przykład 2.7

I .udność pewnego miasta w trzech kolejnych okresach wynosiła odpowiednio: 6 tys., 8 tys., 10 tys. osób. Należy obliczyć przeciętny przy-Mm! względny ludności:

8 10 ₁₀-a, — = 1,33 x, = — = 1,25.

‘6 ² 8

x„ -

30 + 50 + 120 200

30 50 120

5 ⁺ 10 ⁺ 20

= 11,8 zł