0435

437

§ 4. Dodatkowe wiadomości o szeregach potęgowych

Podstawiając to do poprzedniej równości otrzymujemy

3"⁺¹«

3jc"⁺¹

da" L    aoj

Tak więc wzór (28) został udowodniony przez indukcję.

Przejdźmy wreszcie do interesującego nas rozwinięcia funkcji u według potęg x. Przy ustalonym a będzie ono oczywiście miało postać rozwinięcia Taylora [438, 9°]

u = u₀+x-

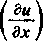
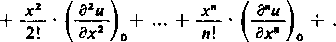
gdzie wskaźnik 0 oznacza, że funkcję i jej pochodne bierzemy w punkcie x — 0. Leczy będzie wtedy równe a, a więc u₀ = f(a), dalej według wzoru (28) jest

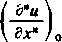
d<f~^l

Podstawiając otrzymane wartości współczynników, otrzymujemy rozwinięcie

(29) f(y) = f(a)+x<p (a)f(a) + - ~ ■ - - [?»-/'(o)] + ... + -£- •    [?>"<«) /'(«)] + ....

2!    n\ dcf~^l

które nazywamy szeregiem Lagrange'a. Jest on ciekawy z tego względu, że jego współczynniki są przedstawione explicite jako funkcje a.

Jeśli f{y) = y, to otrzymujemy w szczególności

(29a)    y = a+x-<p(x)+ ~ • ~~ [ę>²(a)]+ ... + ----^d y [ę>"(o)]+ ...

2! da    n! def-¹

Istnieje ścisły związek między zadaniem rozpatrywanym w tym ustępie, a zadaniem znajdowania szeregu potęgowego dla funkcji odwrotnej. Jeżeli (przy założeniu, że ą> (a)^0) napiszemy równanie (25) w postaci

x =    = b₀+b_i{y-a)+b₂{y-d)²+ ...,

<p(y)

to okazuje się, że zadanie Lagrange’a jest równoważne z odwróceniem tego szeregu ustawionego według potęg y—a. Jeśli przeciwnie, postawimy sobie za zadanie otrzymanie szeregu potęgowego odwrotnego dla szeregu

y = x+a₂ x²+a₂ x³+ ... (flj ^ 0) to napiszemy tę zależność w postaci

y = x iai + a₂ x+a₃ x²+ ...) ,

i oznaczymy sumę szeregu przez y> (x). Dochodzimy wtedy do równania

x = y-

tp(x) ’

postaci (25), gdzie a = 0, <p (x) = l/ę> (*) i prócz tego x i y zamieniły swoje role. Ta ostatnia uwaga jest ważna jeszcze z tego powodu, że pozwala od razu napisać ogólny wzór na wynik odwrócenia według wzoru (29a):

(30)

x = y-

1

y (0)

+

y² \J__L_1    ₊ . + 2l [ ^d'~^l 1 1

2! L dx v²WJ*-0    n\ L y>"(*)J„.o

+