0618

620
XIV. Całki zależne od parametru
Bezpośrednie uzasadnienie tej zmiany wymaga jednak kłopotliwych przekształceń i oszacowań, wobec tego posłużymy się znów czynnikiem uzbieżniającym e~kt (k > 0) (por. punkt 2 tego ustępu).
Będzie teraz
co co 00
f S^— e~kt dt = —f e~kt sin t dt f e~,u2 du
0J V* A oJ 0J
2
A
CO 00
J* du J* e_u+"J)‘ sin t dt o o
2 f du
fir J 1+(*+“2)2 ‘
Tym razem możemy zmienić kolejność całkowania na podstawie twierdzenia 5. Pozostaje jeszcze przejść do granicy przy k -»0, co jak łatwo sprawdzić może być przeprowadzone pod znakiem całki.
Ostatecznie
dt =
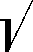
00
Tę samą wartość otrzymamy dla całki
dt. Zatem
f
sm
x2dx = J cos x2 dx = \ ]/
,/Z
523. Przykłady różniczkowania pod znakiem całki.
1) Różniczkując względem parametru a>0 znane całki
(a) / > w/
0 O
dx
a+x2
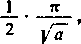
(c) J x°~ldx
O
a
znajdziemy nowe, interesujące całki.
Rozwiązanie, (a) Różniczkując n-krotnie według reguły Leibniza otrzymujemy
(2zi— 1)! 2n+lef
f e-xlx2"dx
Stosowanie tej reguły jest tu dozwolone, ponieważ wszystkie otrzymane w ten sposób całki są zbież-
oo
ne jednostajnie względem a dla a>a0>0; na przykład dla napisanej całki majorantą jest J e~a°*2x2ndx.
o
dx
(.a+x2y
1 (2/1-1)!! J___7C_
2 ‘ (2«)!1 ‘ o* ' y/a ’
nl
a"+l
(c) / X*-1 ln"x dx = (-1)' o
Wyszukiwarka
Podobne podstrony:
570 XIV. Całki zależne od parametru Łatwo jest sprawdzić te wyniki obliczając bezpośrednio
592 XIV. Całki zależne od parametru 3) Dowieść bezpośrednio, że całkaf Are-"^dx J v3 dla
564 XIV. Całki zależne od parametru Konieczność. Jeżeli /(x, y) dąży jednostajnie do <p (x), to d
566 XIV. Całki zależne od parametru równość (4). Ustalmy wartości y i y spełniające warunki (5), a
568 XIV. Całki zależne od parametru Na przykład, nie oblicząjąc całek J In (x2+y2)dx, O widzimy od
572 XIV. Całki zależne od parametru podczas gdy / dxffdy- - iir. 0 o 509. Przypadek gdy granice całk
574 XIV. Całki zależne od parametru niewłaściwym) w przedziale <a, bj. W ten sposób można wyłożon
576 XIV. Całki zależne od parametru można znalezione wyrażenie dla / napisać w postaci /= V(-1)*
578 XIV. Całki zależne od parametru Łatwo jest sprawdzić, że założenia twierdzenia 3 są tu spełnione
580 XIV. Całki zależne od parametru Oczywiście wystarczy sprawdzić, że każda z tych funkcji z osobna
582 XIV. Całki zależne od parametru Ponieważ /„(<?) = 0, więc X /« + iU)=
584 XIV. Całki zależne od parametru 18) Podamy jeszcze przykłady całek, w których nie można zmienić
586 XIV. Całki zależne od parametru§ 2. Zbieżność jednostajna całek 513. Definicja całki zbieżnej
588 XIV. Całki zależne od parametru 515. Warunki dostateczne zbieżności jednostajnej. Podamy teraz p
590 XIV. Całki zależne od parametru 516. Drugi przypadek zbieżności jednostajnej. Rozpatrzmy teraz
594 XIV. Całki zależne od parametru 12) Wykazać to samo dla całki f 8jc3yJ (x* -8 xy3 dx. Tutąj
596 XIV. Całki zależne od parametru n-* co dąży jednostajnie do <p(x) = 0 w całym przedziale <
598 XIV. Całki zależne od parametru Twierdzenie powyższe pozostaje oczywiście prawdziwe, gdy wszystk
600 XIV. Całki zależne od parametru Wobec tego całka z tej sumy jest zbieżna jednostajnie w punktach
więcej podobnych podstron