0626

628

XIV. Całki zależne od parametru

dv

Różniczkujemy teraz całkę v względem a według reguły Leibniza i pochodną -r~ przedstawiamy w postaci

da

*L = _ J§- ( f e-^dz- f    dz).

da    J z²+l I

r*

Stąd dla v otrzymujemy równanie różniczkowe

4L-2o_V=-1.

da

Mnożąc je obustronnie przez czynnik całkujący e~*² dostajemy równość

J-[ve-^,]= -e-¹, da

którą całkujemy względem a od 0 do a. Otrzymujemy w ten sposób

W** = t>₀— / e~‘²dt, o

przez v₀ oznaczona jest wartość graniczna

»o

lim v =

•~o

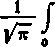
dz

z^ł + l

00

2

00

Ponieważ tę samą wartość ma całka J e~<²dt, więc dla v otrzymujemy wyrażenie

o

v = e*^1, f e~'*dt

e

identyczne z otrzymanym wyżej dla całki u.

12) Udowodnić tożsamość (przy k>0)

f ~^rdx= f

J 1+JE²    ./    X

o    o

Obie całki jako funkcje k spełniają równanie różniczkowe

y"+y = ]-. k

Dla pierwszej całki sprawdzamy to od razu, różniczkując ją dwukrotnie według reguły Leibniza; dla drugiej wygodniej jest skorzystać z przedstawienia jej w postaci

cos    dt-sin * f    dt.

k    k

Różnica z — z (fc) całek stojących po obu stronach tożsamości spełnia zatem równanie jednorodne z"+z = 0, a więc musi mieć postać

z — Ci sin (k+C₂),

Ci i C₂ są stałymi. Obie całki, a wraz z nimi ich różnica z, dążą do 0, gdy £-» oo. Stąd C, = 0, z (k) = 0 i tożsamość jest udowodniona.