0664

666

XIV. Całki zależne od parametru

2) Ze wzoru (23)

IM

r(a)

1    1 dx

(! + *)* J *

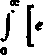
wyprowadzić bezpośrednio wzór (24)

r'(a)

r(a) J L u

O

i—e~

]

du.

Zauważmy, że trudność leży w tym, że całki (24) nie można traktować jako różnicy dwu całek. W przeciwnym przypadku przekształcenie drugiej całki za pomocą podstawienia x = «"—1 dawałoby od razu żądany wynik.

Obchodząc tę trudność obliczamy

r /»

M_=limjr £Z*L- f -    —-1 = lim 1JlOŚiL—    f    A ₌

(a) ,.₀ V x J (1 +jc)*jr J _M J u J 1-e-" j

et    t    ln(i+t>

I    O

ponieważ

*

lim | —--du — 0.

e-*o J l—e~^m

lo(l+«)

To zaś wynika z oszacowania tej całki przez

e—ln (1+e) . e

«(1+e)"-¹    2(l+£)"-‘

3) Wychodząc z następującej definicji stałej Eulera:

C = lim

udowodnić następujące wzory całkowe:

(a) C= f (1-e-*) — - f €~~^x —,    (b) C= f (-1--<r") —.

./    X j X    J \l+u fu

Ponieważ oraz

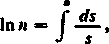
t