0656

658

XIV. Całki zależne od parametru

8) Udowodnić, że

t    <o

/ (1 -x³)~¹'³dx = j/T/ (*³-l    .

—® 1

Rozwiązanie. Oznaczmy

1 00 / (l-x³)^lt2dx = /,,    / (x³—i)~^,l2dx = /₂ ,

O    1

/ (l-jc³)-^,/3<fe = J (1 +x³)~^t>³dx = /,.

•0    O

Należy udowodnić równość

h+i₃ = Vfh.

Stosując do tych całek odpowiednio podstawienia x = t^ll3,x = t~^ll3,x — (/-^I — l)^,/3 sprowadzimy je do całek Eulera pierwszego rodząju. Następnie trzeba tylko kilkakrotnie zastosować wzór na dopełnienie.

9) Udowodnić wzór (wyprowadzony przez Dirichleta)

r«/

O

_e-/x_x—¹

(g+xY

dx

o

<f+yy

dy

(/. s,g,r> O) .

Wskazówka. Podstawić

T(r)

(?+*)'

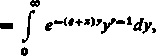
r(s)

(f+yy

co

= f e-^(f+»x’-'dx o

i zmienić kolejność całkowania względem x i y (przypadek funkcji dodatniej).

10) W zadaniu 12) z ustępu Sil udowodniliśmy tożsamość

EK‘+E‘K-1nr = c = const

(oznaczenia podane są w cytowanym miejscu). Następnie, stosując pewne przejście graniczne pokazaliśmy, że c =* 7t/2. Ten sam wynik można uzyskać obliczając wartość lewej strony dla jakiejkolwiek wartości

Niech k = l/j/2, wtedy k’ =k, E’ =Ei K’ = Ki tożsamość przybiera postać

1EK-K³ = (2E—K)‘K «= c .

Całki

TC/2    rt/2 _

*- ] —/T^rr-T ’    ^£=/    2"^sin2W dtp

o yl-jsin³ę>    o

można sprowadzić przez kolejne podstawienia cos <p = t, t* — x do całek Eulera pierwszego rodząju;

1

K = -1^- f *^-3/4(l-x)-³>³dx

2_V2 i

E

4}/2

|J x-^3/4(1-x)-ⁱ'Vjc+ J