0670

672

XIV. Całki zależne od parametru

Jeśli przyjmiemy a — y i podstawimy x = t², to będziemy mieli

/ e~^,lln t dt - i r (j) = -    (C+2 In 2),

o    ⁴

co z łatwością możemy obliczyć z rozwinięcia (27), korzystając przy tym z własności szeregu logarytmicznego.

Różniczkując powtórnie względem a doszliśmy do równości (8'):

r"(a) = f x-^fe-* ln^ł * dx.

O

Dla a = 1 daje ona:

f <--* In¹* dx = r'(l) = C^ł+ —.

i    ⁶

Ten wynik można otrzymać z (28), jeżeli się posłużyć przy tym znanym szeregiem

30

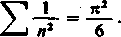
1

Wreszcie, przyjmując i tutaj a = -j i podstawiając x = t², otrzymamy taką jeszcze całkę

/ e-‘*ln²tdt    [(C+2 In 2)*+ -yj ,

i tak dalej.

2) Obliczyć całkę

/ = f^Ldx,

J x o

gdzie p jest ułamkiem o nieparzystym liczniku i mianowniku.

Wskazówka. Posłużyć się wzorem Łobaczewskiego [497, 14)]; zgodnie z nim

/= J sin’-'xdx

o

[por. 532, 4 (b)]. Odpowiedź:

/ = l£L . ^rW²> _ ,„.2 ir(p/2)i² 2 r [^p+1 j ^(p)

3) Obliczyć całki (ó>0):

OO    00

r ęosb±_dx (Ocscl), 8= f    (0<s<2).

J x*    J x“

COSÓJC J_ m ^    ^    n f sini*

Jest [por. (13)]

— =    f z‘~'e~‘^xdz,

x* r (i) J