Struik 010

zachovalo jen m£lo. Naśe znalosti orientalni matematiky jsou proto vełmi utrżkovite; pro stale ti pred rozvojem recke vedy jsme odkśzani skoro vylucne na materiśl z Mezopotamie nebo Egypta. Je tedy docela dobre możne, że by nove objevy mohly vest k tiplne novemu hodnoceni vyzhamu rftznych forem orientalni matematiky. Dlouhou dobu były naśe nejbohatśi historicke prameny z Egypta,. a to z toho ddvodu, że jiż roku 1858 byl objeven tzv. Rhinduv papyrus, ktery byl napsan jiste pred rokem 1650 pred n. L, ale obsahuje materiał mnohem starsi. V poślednich triceti letech se mimoradne rozśirily naśe znalosti babylónske matematiky diky pozoruhodnym objevum O. Neugebauera a F. Thureau-Dangina, kteri rozluśtili velky poćet hlinenych tabulek. Zda se nyni, jako by se matematika Babylóńanu rozvinuła mnohem dśle neż ma-tematika jejich vychodnich souperd. Tento tisudek budę asi spravny, nebot v obsahu babyłónskych a egyptskych textu existovała po staleti jistś vnitrni souvislost. K tomu ekonomicky vyvoj v Mezopotamii opet postoupił dśle neż v ostatnich zemich te urodne casti Blizkeho vychodu, kte-ra se tśhne od Mezopotamie do Egypta. Mezopotamie była kriżovatkou velkeho poctu karavannich cest, zatimco Egypt meł pomerne izolovanou polohu. K tomu pristupuje jeśte okolnost, że regulace nevypo5itatelneho Tigridu a Eufratu vyżadovala mnohem vice technicke zrucnosti a technickych opatreni neż Nil, „nejvetśi gentleman mezi vśemi rekami*^{1 2}, abychom poużili slov Sira Williama Will-cockse. Dalsi badani v stare matematice oblasti Indu mo-hou poskytnout jeśte neocekśvane objevy, ackoli dnes toto tvrzeni nezni jeśte dost presvedcive.

z rimske numerace, kterd spociva na temź principu: MDCCCLXXVIII = 1878. Na zśklade tohoto systemu rozvi-nuli Egyptane aritmetiku prevaźne aditivniho charakteru, coż znamend, źe se snazila hłavne o prevedenf vseho nasobeni na opakovane scitanL Napr. nasobeni 13 se pro-vddelo tak, źe se nejprve nasobilo dvema, pak ctyrmi, pak ósmi a vysledky nasobeni ctyrmi a ósmi se pricetly k danemu cislu.

Pr lklad vypoctu 13 X11:

*1 11 2 22 *4    44

*8 88

Y^sledky oznacend * se sećtou, coź ddvd 143.

Mnoho problemu było velmi jednoduchych, neprekra-cujicich linearni rovnice o jedne nezndme. Tak je tomu v tomto pripade:

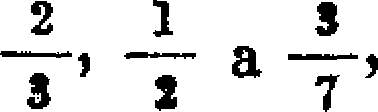
Pricti k velićine jeji velicina ?

obdrźis 33. Jakd je to

Nejvyraznejsim rysem egyptske matematiky było po-cltan! se zlomky. Vsechny zlomky se prevddely na soucty tzv. kmenovych ziomku, tj. ziomka s ćitatelem rovnym 1.

2    1

Jedinou vyjimku tvori!v — = 1--; pro tento ziomek

3    3

se pouźlval zvłdstni symbol. Prevddeni na soudty kmeno-vych zlomkii umoźńovaly tabulky udavajici rozkłady

2

ziomku tvaru —, tedy jedinś rozkłady potrebne pro nd-

n

sobeni dvema. Rhinduv papyrus obsahuje tabulku, kterd udava pro vsechna licha n od 5 do 331 rozkłady ziomku 2

—, na kmenove zlomky, napr. n

2_ _    1    1    2    _ 1 1 1

7    4    28*    97    56    679    776 *

Tento zpusob pocitdni se zlomky vtiskl egyptske matematice komplikovany a teźkopddny raz a trvale zabrdnil dal-

21

1

Vetśina naśich znalosti o egyptske matematice pra-

2

meni ze dvou matematickych papyru: je to jednak jiż zmineny Rhinduv papyrus, obsahujici 85 uloh; jednak tak-zvany Moskevsky papyrus, ktery je asi o dve stoleti starśi a obsahuje 25 uloh. Tyto ułohy były vykladany uż dlouho pred vznikem rukopisO; prece vśak existuji papyrusy menśiho rozsahu z podstatne mladśich dob — dokonce z doby rimske — ktere nejsou metodicky nijak odłiśne. Matematika vykladana v obou techto papyrusech se opirś o desitkovy pocetni system se zvlśśtnim znakem pro każ-dou vetśi decimślni jednotku. Tento system zname dobre