Analiza5 jpeg

220 Metody oceny efektyności projektów inwestycyjnych

220 Metody oceny efektyności projektów inwestycyjnych

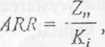
(5.2)

gdzie Z„ — średnioroczny zysk netto obliczony z całego okresu realizacji danego przedsięwzięcia, K, - wartość kapitału wykorzystywanego do sfinansowania początkowych nakładów inwestycyjnych.

Istnieje wiele sposobów wyznaczania ARR. W zależności od tego, jakie wielkości występują w liczniku i mianowniku (5.2), można księgową stopę zwrotu zdefiniować jako

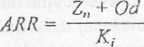
(5.3)

lub (5-4) gdzie Od - roczne odsetki od kr edytów, K_w - nakład inwestycyjny finansowany kapitałem własnym lub taka część nakładu, jaka jest finansowana kapitałem własnym. Księgowa stopa zwrotu (5.4) zwana jest także wskaźnikiem stopy zwrotu Z inwestycji {Return on Invcs(ment -ROI).

. Księgowa stopa zwrotu jest wykorzystywana do oceny rentowności pojedynczych projektów inwestycyjnych lub wyboru najbardziej opłacalnego projektu spośród dostępnych. W pierwszym przypadku należy realizować ten projekt, dla którego ARR jest większe od granicznej księgowej stopy zwrotu określonej na podstawie rynkowej stopy procentowej, a w drugim ten projekt, który wykazuje największą wartość ARR.

Przykład 5.2. .Taka jest rentowność dwóch pięcioletnich projektów inwestycyjnych, dla których oszacowane wartości zysku netto w poszczególnych latach trwania inwestycji wynoszą:

Lala	I	2	3	4	5
Projekt A	3125	3320	3254	3424	3500 '
Projekt B	3000	3300	3500	3400	3200

Oba projekty wymagają takich samych nakładów w wysokości 12 000 zł. W. przypadku projektu A inwestycja będzie finansowana z kapitału własnego w wysokości 6000 zł i kredytu w kwocie 6000 zł. W przypadku projektu B inwestycja będzie finansowana z kapitału własnego w wysokości 5000 zł i kredytu w kwocie 7000 zł. Określona przez inwestora graniczna stopa rentowności wynosi 25%.

Na podstawie danych otrzymuje się. następujące wartości średniorocznych zysków netto:

3125 + 3320 + 3254 4 3424 t- 3500

Wewnętrzne stopy zwrotu dla poszczególnych projektów wynoszą:

Pp h, II	3324,6		AKR^0 =	3280	= 0,27 (wg (5.2)),
	12 000	- U,Z o,		i 2 000
ARR^a =	3324,6 6000	= 0,55,	ARR" =	3280 5000	= 0,66 (wg (5.4)).

— - 3324,6, Z„ =• 3280.

Z obliczeń wynika, że. realizacja obydwu projektów inwestycyjnych będzie dla inwestora opłacalna.

Metoda ARR nic uwzględnia zmian wartości pieniądza w czasie. Zdaniem E.F. Brighama i L.C. Gapenskiego należy ją raczej wykorzystywać do mierzenia wyników osiąganych przez różne działy w danej firmie, a nie w celu podejmowania decyzji o preliminowaniu inwestycji⁴.

5.2. Dynamiczne (dyskontowe) metody oceny projektów inwestycyjnych

Cechą charakterystyczną dynamicznych metod oceny projektów inwestycyjnych jest stosowanie rachunku dyskontowego do porównywania wydatków i wpływów związanych z dauym projektem inwestycyjnym. Ważną zaletą lycli metod jest lo, że pozwalają porównać projekty inwestycyjne w dowolnym okresie funkcjonowania przedsięwzięcia. Fakt ten z jednej strony sprzyja dokładności oceny opłacalności inwestycji, z drugiej zaś narzuca na podmiot konieczność dokładniejszego prognozowania stóp procentowych oraz wnikliwsze ocenianie sytuacji finansowej i gospodarczej, w której będzie funkcjonował.

W dynamicznych metodach oceny projektów inwestycyjnych jako wartość stopy dyskontowej przyjmuje s.ię koszt kapitału (koszt alternatywny). Koszt ka pilału jest to taka stopa zwrotu (stopa zysku), którą firma musi uzyskać z tytułu realizacji swoich inwestycji, aby jej wartość lyukowa nie uległa zmianie. Koszt kapitału może być również interpretowany jako stopa z inwestycji, której spodziewają się wierzyciele fumy. W celu oszacowania kosztu kapitału stosuje się dwa podejścia⁵:

— w pierwszym przyjmuje się, żc koszt kapitału równy jesL stopie zwrotu, która może być osiągnięta na rynku z inwestycji o podobnym ryzyku jak rozpatrywany projekt;

⁴ E.F. Brigbara, L.C. Gapr.nski, Zarządzanie finansami, t. 1, FWE, Warszawa 2000, s. 30.1. ³ Matematyka i statystyka finansowa, E. Nowak (red.), FK.R, Warszawa 1997, s. 72.