23 luty 07 (91)

ostatecznie

d²l

^aB2B3 =—f = lie₁sin((p₁-<p₃) + li(D?cos((p₁-(p₃) + l₃a)§    (P2.88)

dt

Obracając układ współrzędnych o kąt (<p₃ -90°) otrzymamy przyspieszenie kątowe jarzma

- IfE-, sin( <p₁-(p₃ + 90° )-li(Oi cos( <p₇ ~(p₃ +90°)+

+ cos((p₃ -ę₃ +90° )-2^-co₃sin(ę₃ -<p₃+90°)-    (P2.89)

dr    dt

-I₃e₃ sin(ę₃-(p₃+ 90° )-l₃(o₃ cos((p₃-cp₃+90° ) = 0

ostatecznie otrzymujemy

e₃ = ~~7~ cos((pi — (p₃) + -l-(0² sin((pi — (p₃) —    (P2.90)

l₃    l₃    dt l₃

Przykład 2.10

Mechanizm złożony

Analiza kinematyczna mechanizmu złożonego zostanie pokazana na przykładzie mechanizmu napędu stołu strugarki przedstawionego w postaci schematu na rysunku 2.32.

Rozwiązanie

Po przeprowadzeniu analizy strukturalnej zauważymy, że mechanizm składa się z członu napędzającego 1 oraz dwóch grup strukturalnych połączonych szeregowo. W związku z tym analiza parametrów kinematycznych grupy (4, 5) mechanizmu korbowo-suwakowego, jest możliwa po uprzedniej analizie grupy (2, 3) mechanizmu jarzmowego.

Zadanie można zatem rozwiązać w dwóch etapach.

Etap 1

Analiza mechanizmu jarzmowego opisanego wielobokiem wektorowym

h ⁺h⁺!o ⁼ 0    (P2.91)

Dane: li,<Pi(t),l₀,<Po =90°.

Obliczyć: l₃,cp₃

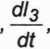
003,

d²l₃

dt²

,e₃.

89