23 luty 07 (97)

2

2^; t////i\	\v///a
v//sx\	IY///A
1___■
Y///AI	ir////i
Y777M	\V77A

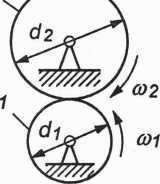
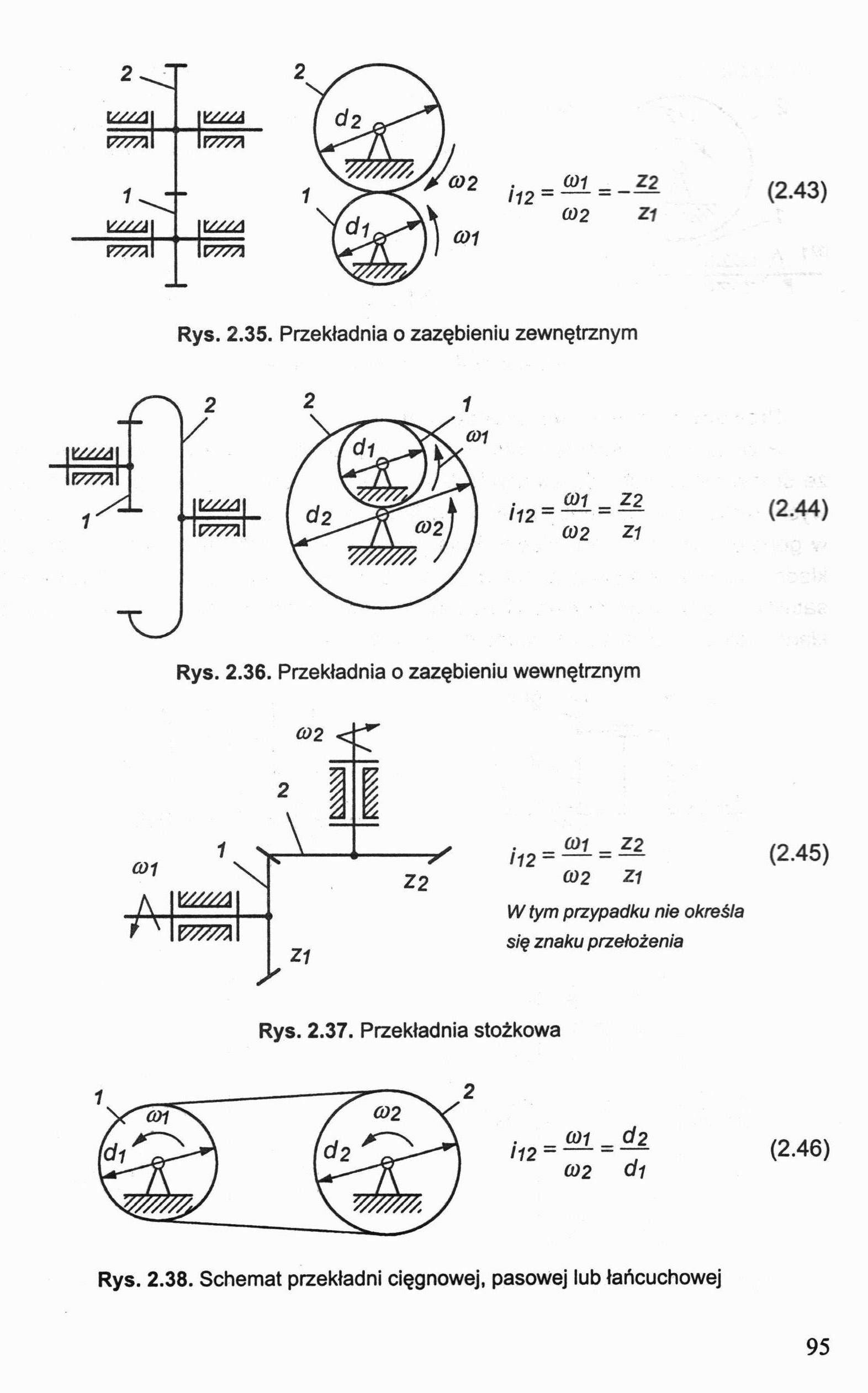
(01 _ _Z2 (02 Z1

(2.43)

Rys. 2.35. Przekładnia o zazębieniu zewnętrznym

2 1

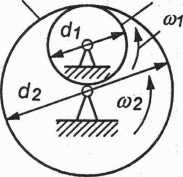
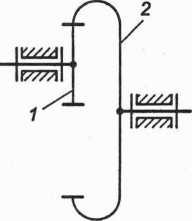
(01 _ Z2 (02 Z1

(2.44)

Rys. 2.36. Przekładnia o zazębieniu wewnętrznym

(2.45)

.    _(01 _Z2

112--- —

(02 Z1

W tym przypadku nie określa się znaku przełożenia

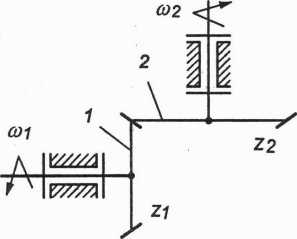
Rys. 2.37. Przekładnia stożkowa

(2.46)

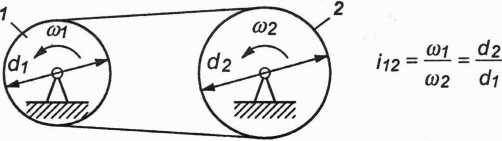
Rys. 2.38. Schemat przekładni cięgnowej, pasowej lub łańcuchowej

95