243 [1024x768]

250 PODSTAWY TERMODYNAMIKI CHEMICZNEJ

oraz wyrażeniem na energię wewnętrzną (3.170)

III ZASADA TERMODYNAMIKI

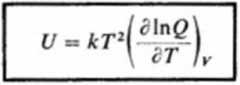
otrzymujemy:

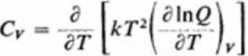
Bardziej szczegółową postać równania (3.179) otrzymamy przy omawianiu sum stanów dla poszczególnych rodzajów energii.

Obliczenie entropii molowej S. Entropia molowa S związana jest z ciepłem molowym za pomocą równości

T

s-s₀ = [-?- ar

0

Po wstawieniu w to równanie wyrażenia na C_v (3.179), należy przeprowadzić całkowanie przez części:

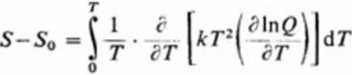
Ł/

7*

+&ln(2-fcln@<r_f,o)

Ponieważ dla jednego mola czystej substancji w 0 K. wielka suma stanów wynosi zgodnie z równaniem (3.172)

/

(?(T.Oł- X^g| C'^ł,,/łT mgo m 1 m

zatem

S₀ = k\nQ = k ln£₀ = 0 i ostatecznie

5-y+Arłn0

(3.180)

(3.181)

Równanie (3.180) jest w istocie statystycznym uzasadnieniem tzw. trzeciej zasady termodynamiki, wg której entropia wszystkich czystych substancji krystalicznych w temperaturze 0 K jest równa zeru.

Energię swobodną rozważanego układu otrzymamy z. zależności (3.37)

F — U—TS